Показатель несжимаемости / устойчивости к сжимаемости вещества.
Иллюстрация равномерного сжатия
Объемный модуль упругости
( или ) вещества является мерой того , насколько устойчивым к сжатию , что вещество. Он определяется как отношение бесконечно малого увеличения давления к результирующему
относительному
уменьшению объема . [1] Другие модули описывают реакцию материала ( деформацию ) на другие виды напряжения : модуль сдвига описывает реакцию на сдвиг, а модуль Юнга описывает реакцию на линейное напряжение. Для жидкости значение имеет только модуль объемной упругости. Для сложного анизотропного твердого тела, такого как K {\ displaystyle K} B {\ displaystyle B} дерево или бумага , эти три модуля не содержат достаточно информации, чтобы описать его поведение, и необходимо использовать полный обобщенный закон Гука .
Определение [ править ]
Объемный модуль упругости можно формально определить уравнением K > 0 {\ displaystyle K> 0}
K знак равно — V d п d V {\ displaystyle K = -V {\ frac {dP} {dV}}}
где — давление, — начальный объем вещества, а обозначает производную давления по объему. Учитывая единицу массы, п {\ displaystyle P} V {\ displaystyle V} d п / d V {\ displaystyle dP / dV}
K знак равно ρ d п d ρ {\ Displaystyle К = \ ро {\ гидроразрыва {дП} {д \ ро}}}
где ρ
— начальная плотность, а d
P
/ d
ρ
обозначает производную давления по плотности (т.е. скорость изменения давления в зависимости от объема). Обратный модуль объемного сжатия дает сжимаемость вещества .
Механические свойства
Только при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала. А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры:
Читать также: Вакуумный насос своими руками в домашних условиях
- Жёсткостью называют произведение поперечного сечения профиля на модуль упругости. По этой величине можно судить о пластичности узла конструкции в целом, а не о материале отдельно. Единицей измерения являются килограммы силы.
- Продольное относительное удлинение — это отношение абсолютного удлинения материала-образца к его общей длине. К примеру, на стержень, длина которого равна 200 миллиметров, приложили некоторую силу. В результате он стал короче на 5 миллиметров. В результате относительное удлинение будет равняться 0,05. Эта величина безразмерная. Для более удобного восприятия иногда её переводят в проценты.
- Поперечное относительное удлинение рассчитывается точно так же, как и продольное относительное удлинение, но вместо длины берут диаметр стержня. Опытным путём было установлено, что для большего количества материала поперечное меньше продольного удлинения приблизительно в 4 раза.
- Коэффициент Пуассона. Это отношения относительной продольной к относительной поперечной деформации. При помощи этой величины можно полностью описать под воздействием нагрузки изменения формы.
- Модуль сдвига описывает упругие свойства под воздействием касательных свойств на образец. Иными словами, когда вектор силы направляется к поверхности тела под 90 градусов. Примером подобных нагрузок служит работа гвоздей на смятие, заклёпок на срез и пр. Этот параметр связан с вязкостью материала.
- Модуль упругости объёмной характеризует изменение объёма образца для разностороннего равномерного приложения нагрузки. Эта величина является отношением давления объёмного к деформации сжатия объёмной. Как пример можно рассматривать опущенный в воду материал, на который воздействует давление жидкости по всей его площади.
Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства. Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.
У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.
Термодинамическое соотношение [ править ]
Строго говоря, объемный модуль упругости является термодинамической величиной, и для того, чтобы указать объемный модуль, необходимо указать, как давление изменяется во время сжатия: постоянная температура (изотермическая ), постоянная энтропия ( изэнтропическая ) и другие варианты возможны. . Такие различия особенно актуальны для газов . K Т {\ displaystyle K_ {T}} K S {\ displaystyle K_ {S}}
Для идеального газа изэнтропический процесс имеет:
п V γ знак равно c о п s т . ⇒ п ∝ ( 1 V ) γ ∝ ρ γ , {\ Displaystyle PV ^ {\ gamma} = const. \, \ Rightarrow P \ propto \ left ({\ frac {1} {V}} \ right) ^ {\ gamma} \ propto \ rho ^ {\ gamma}, }
поэтому изоэнтропический модуль объемной упругости определяется как: K S {\ displaystyle K_ {S}}
K S знак равно γ п . {\ displaystyle K_ {S} = \ gamma P.}
Точно так же изотермический процесс идеального газа имеет:
п V знак равно c о п s т . ⇒ п ∝ 1 V ∝ ρ , {\displaystyle PV=const.\,\Rightarrow P\propto {\frac {1}{V}}\propto \rho ,}
поэтому изотермический модуль объемной упругости определяется выражением K T {\displaystyle K_{T}}
K T = P {\displaystyle K_{T}=P}
где γ
представляет собой отношение теплоемкости и
р
является давлением.
Когда газ не идеален, эти уравнения дают только приближение модуля объемного сжатия. В жидкости объемный модуль K
и плотность
ρ
определяют скорость звука
c
( волны давления ) в соответствии с формулой Ньютона-Лапласа
c = K ρ . {\displaystyle c={\sqrt {\frac {K}{\rho }}}.}
В твердых телах и имеют очень похожие значения. Твердые тела также могут выдерживать поперечные волны : для этих материалов требуется один дополнительный модуль упругости , например модуль сдвига, для определения скорости волны. K S {\displaystyle K_{S}} K T {\displaystyle K_{T}}
Общее понятие
При любом внешнем воздействии на предмет, внутри его возникают встречные силы, компенсирующие внешние. Для идеальных систем, находящихся в равновесии, силы равномерно распределены и равны, что позволяет сохранить форму предмета. Реальные системы не подчиняются таким правилам, что может привести к их деформации. Оценивая прочность материалов, говорят об их упругости.
Определение модуля Юнга твердых тел
Упругие материалы – это те, которые после прекращения внешнего воздействия, восстанавливают свою первоначальную форму.
Внутренние силы распределены равномерно по всей площади поперечного сечения предмета, имеют свою интенсивность, которая выражается количественно, называется напряжением (р) и измеряется в Н/м2 или по международной системе Па.
Напряжение имеет свою пространственную направленность: перпендикулярно площади сечения предмета – нормальное напряжение (σz) и лежащая в плоскости сечения – касательное напряжение (τz).
Опыт с пружинными весами
Модуль упругости (Е) как единицу измерения отношения материала к линейной деформации, и нормальное напряжение связывает формула закона Гука:
ε = σz/E (1)
где ε – относительное удлинение или деформация.
Преобразовав формулу (1) для выражения из нее нормального напряжения, можно увидеть, что Е является постоянной при относительном удлинении, и называется коэффициентом жесткости, а его единицы измерения Па, кгс/мм2 или Н/м2:
σz = Eε (2)
Модуль упругости – это единица измерения отношения напряжения, создаваемого в материале, к линейной деформации, такой как, растяжение и сжатие.
В справочных материалах размерность модуля упругости выражается в МПа, так как деформация имеет довольно малое значение. А зависимость между этими величинами обратно пропорциональная. Таким образом, Е имеет высокое значение, определяемое 107-109.
Выбранные значения [ править ]
Приблизительный модуль объемной упругости (K) для обычных материалов
| Материал | Объемный модуль в ГПа | Магистральный модуль в МПСИ |
| Резина [2] | 1,5 к2 | От 0,22 до0,29 |
| Натрия хлорид | 24,42 | 3,542 |
| Стекло (см. Также схему под таблицей) | От 35 до55 | 5,8 |
| Стали | 160 | 23,2 |
| Diamond (в разрешении 4K) [3] | 443 | 64 |
| Гранит | 50 | 7.3 |
| Сланец | 10 | 1.5 |
| Известняк | 65 | 9,4 |
| Мел | 9 | 1.3 |
| Песчаник | 0,7 | 0,1 |
Влияние добавок выбранных стеклянных компонентов на модуль объемной упругости определенного базового стекла. [4]
Материал с объемным модулем упругости 35 ГПа теряет один процент своего объема при воздействии внешнего давления 0,35 ГПа (~3500 бар ).
Приблизительный модуль объемной упругости (K) для других веществ
| Вода | 2,2 ГПа (значение увеличивается при повышении давления) |
| Метанол | 823 МПа (при 20 ° C и 1 Атм) |
| Воздуха | 142 кПа (адиабатический объемный модуль [или изоэнтропический объемный модуль]) |
| Воздуха | 101 кПа (изотермический модуль объемной упругости) |
| Твердый гелий | 50 МПа (приблизительно) |
Факторы, влияющие на значение расчетного модуля упругости
Более подробно сущность модуля упругости, предела пропорциональности, предела прочности, нормальных напряжений, деформаций и других понятий рассматривается отдельно. Здесь лишь отметим, что для материалов, у которых предел пропорциональности незначительно меньше предела текучести, можно использовать линейную деформационную модель. Т.е. предполагать деформации прямо пропорциональными нормальным напряжениям.
Читать также: Латунь ржавеет или нет
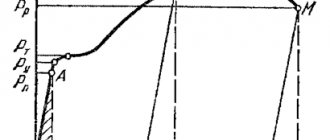
Примером таких материалов являются стали различных марок. А вот бетон к таким материалам не относится. Более того, у бетона нет ярко выраженного предела пропорциональности и предела текучести. Диаграмма напряжений бетона при постепенном загружении выглядит приблизительно так:
Рисунок 324.1
Однако это далеко не единственная из возможных диаграмм напряжений бетона, так как на значение деформаций ε будут влиять не только нормальные напряжения σ, возникающие в поперечных сечениях, но и множество других факторов:
Класс бетона
Начальный модуль упругости бетона зависит от класса бетона. Значение начального модуля упругости можно определить по следующей таблице:
Таблица 1. Начальные модули упругости бетона (согласно СП 52-101-2003)
Время приложения нагрузки
При кратковременном действии нагрузки деформации бетона почти прямо пропорциональны напряжениям, кроме того такие деформации остаются упругими. При расчетах на кратковременное действие нагрузки (до 1-2 часов) значение приведенного модуля упругости на участках без трещин определяется по формуле:
где φb1 = 0.85 – для тяжелых, мелкозернистых и легких бетонов на плотном мелком заполнителе; = 0.7 – для поризованных и легких бетонов на пористом мелком заполнителе.
При длительном действии нагрузки того же значения, деформации начинают увеличиваться до некоторого предела, например при σ = Rb – до точки 1 на диаграмме напряжений. После снятия нагрузки пластические деформации εпл останутся (потому они пластическими и называются), а при повторном загружении до указанного предела деформации будут прямо пропорциональны напряжениям. Процесс нарастания пластических деформаций с течением времени при постоянных нормальных напряжениях называется ползучестью бетона.
Так как при длительном действии нагрузки диаграмма напряжений стремится к показанной на рисунке 324.1, то при расчетах необходимо учитывать нелинейность изменения деформаций при линейно изменяющихся напряжениях. К тому же в изгибаемых элементах нелинейному изменению деформаций препятствует сам материал. Напомню, нормальные напряжения в поперечных сечениях изгибаемых элементов прямо пропорциональны расстоянию от центра тяжести сечения, через который проходит нейтральная линия, до рассматриваемой точки. Таким образом различные слои бетона, работающие совместно, приводят к частичному перераспределению деформаций по высоте элемента, при этом перераспределенную эпюру деформаций можно условно рассматривать как линейную:
Рисунок 324.2
На рисунке 324.2 показана некоторая высота сжатой зоны сечения у, при которой нормальные напряжения σ будут прямо пропорциональны расстоянию от центра тяжести до рассматриваемой точки, это соответствует работе бетона в области условно упругих деформаций. При этом изменение деформаций можно рассматривать по зависимости, показанной на рисунке 324.2.а) или 324.2.б). Часто расчетами на прочность допускается наличие в сжатой области пластического шарнира, при котором изменяется эпюра напряжений и соответственно увеличивается значение деформаций:
Рисунок 324.3
На основании этого для упрощения расчетов обычно принимается двухлинейная (рис. 324.3. а) или трехлинейная (рис. 324.3.б) диаграмма состояния сжатого бетона. Согласно СП 52.101.2003 трехлинейная диаграмма выглядит так:
Читать также: Как обозначаются сварные швы на чертежах
Рисунок 324.4
Еb1 – при кратковременном действии нагрузки принимается равным Eb, а при длительном действии нагрузки определяется по следующей формуле:
где φb,cr – коэффициент ползучести бетона, определяемый в зависимости от класса бетона и влажности окружающей среды. Таким образом учитывается третий фактор, влияющий на модуль упругости бетона:
Влажность воздуха
Значение коэффициента ползучести определяется по следующей таблице:
Таблица 2. Коэффициенты ползучести бетона
а значения деформаций εbo и εb2 при необходимости (если нормальные напряжения больше 0.6Rb,n) определяются по таблице 3:
Таблица 3. Относительные деформации бетона (согласно СП 52-101.2003)
На значение модуля упругости бетона также влияют температура окружающей среды и интенсивность радиоактивного излучения.
Значение начальных модулей упругости, приведенных в таблице 1, соответствует температуре окружающей среды +20±5 о С и нормальному радиационному фону. При изменении температуры в пределах ±20 от указанного значения влияние температуры на модуль упругости можно не учитывать. А при больших изменениях температуры следует учитывать еще и температурные деформации бетона. В целом уменьшение температуры приводит к увеличению модуля упругости, но и к повышению хрупкости материала, а увеличение температуры – к уменьшению модуля упругости и к увеличению пластичности материала.
А теперь попробуем выяснить, как все эти теоретические цифры можно применить на практике.
Микроскопическое происхождение [ править ]
Межатомный потенциал и линейная эластичность [ править ]
Межатомный потенциал и сила
Поскольку линейная эластичность является прямым результатом межатомного взаимодействия, она связана с растяжением / сжатием связей. Затем его можно вывести из межатомного потенциала кристаллических материалов. [5] Во-первых, давайте рассмотрим потенциальную энергию двух взаимодействующих атомов. Начиная с очень далеких точек, они почувствуют влечение друг к другу. По мере приближения друг к другу их потенциальная энергия будет уменьшаться. С другой стороны, когда два атома находятся очень близко друг к другу, их полная энергия будет очень высокой из-за отталкивающего взаимодействия. Вместе эти потенциалы гарантируют межатомное расстояние, при котором достигается минимальное энергетическое состояние. Это происходит на некотором расстоянии a 0 , где полная сила равна нулю:
F = − ∂ U ∂ r = 0 {\displaystyle F=-{\partial U \over \partial r}=0}
Где U — межатомный потенциал, а r — межатомное расстояние. Это означает, что атомы находятся в равновесии.
Для того, чтобы расширить два атома подойти в твердое тело, рассмотрит модель простой, скажем, 1-D массив одного элемента с межатомным расстоянием A A, и равновесное расстояние 0 . Его потенциальная энергия-межатомное расстояние связь имеет аналогичную форму , как и случае два атома, который достигает минимально в виде
0 , разложение в ряд Тейлора для этого является:
u ( a ) = u ( a 0 ) + ( ∂ u ∂ r ) r = a 0 ( a − a 0 ) + 1 2 ( ∂ 2 ∂ r 2 u ) r = a 0 ( a − a 0 ) 2 + O ( ( a − a 0 ) 3 ) {\displaystyle u(a)=u(a_{0})+\left({\partial u \over \partial r}\right)_{r=a_{0}}(a-a_{0})+{1 \over 2}\left({\partial ^{2} \over \partial r^{2}}u\right)_{r=a_{0}}(a-a_{0})^{2}+O\left((a-a_{0})^{3}\right)}
В состоянии равновесия первая производная равна 0, поэтому доминирующий член — квадратичный. Когда смещение невелико, члены более высокого порядка следует опускать. Выражение становится:
u ( a ) = u ( a 0 ) + 1 2 ( ∂ 2 ∂ r 2 u ) r = a 0 ( a − a 0 ) 2 {\displaystyle u(a)=u(a_{0})+{1 \over 2}\left({\partial ^{2} \over \partial r^{2}}u\right)_{r=a_{0}}(a-a_{0})^{2}} F ( a ) = − ∂ u ∂ r = ( ∂ 2 ∂ r 2 u ) r = a 0 ( a − a 0 ) {\displaystyle F(a)=-{\partial u \over \partial r}=\left({\partial ^{2} \over \partial r^{2}}u\right)_{r=a_{0}}(a-a_{0})}
Это явно линейная эластичность.
Обратите внимание, что вывод выполняется с учетом двух соседних атомов, поэтому коэффициент Хука равен:
K = a 0 ∗ d F d r = a 0 ( ∂ 2 ∂ r 2 u ) r = a 0 {\displaystyle K=a_{0}*{dF \over dr}=a_{0}\left({\partial ^{2} \over \partial r^{2}}u\right)_{r=a_{0}}}
Эта форма может быть легко расширена до трехмерного случая с объемом на атом (Ω) вместо межатомного расстояния.
K = Ω 0 ( ∂ 2 ∂ Ω 2 u ) Ω = Ω 0 {\displaystyle K=\Omega _{0}\left({\partial ^{2} \over \partial \Omega ^{2}}u\right)_{\Omega =\Omega _{0}}}
Связь с атомным радиусом [ править ]
Как было установлено выше, объемный модуль напрямую связан с межатомным потенциалом и объемом, приходящимся на атом. Мы можем дополнительно оценить межатомный потенциал, чтобы связать K
с другими свойствами. Обычно межатомный потенциал может быть выражен как функция расстояния, которая имеет два члена: один член для притяжения, а другой — для отталкивания.
u = − A r − n + B r − m {\displaystyle u=-Ar^{-n}+Br^{-m}}
Где A
> 0 представляет член притяжения, а
B
> 0 представляет отталкивание. n и m обычно являются целыми, а
m
обычно больше
n
, что отражает характер отталкивания на короткие расстояния. В положении равновесия
u
минимально, поэтому производная первого порядка равна 0.
( ∂ u ∂ r ) r 0 = A n r − n − 1 + − B m r − m − 1 = 0 {\displaystyle \left({\partial u \over \partial r}\right)_{r_{0}}=Anr^{-n-1}+-Bmr^{-m-1}=0} B A = n m r 0 m − n {\displaystyle {B \over A}={n \over m}r_{0}^{m-n}} u = − A r − n ( 1 − B A r n − m ) = − A r − n ( 1 − n m r 0 m − n r n − m ) {\displaystyle u=-Ar^{-n}\left(1-{B \over A}r^{n-m}\right)=-Ar^{-n}\left(1-{n \over m}r_{0}^{m-n}r^{n-m}\right)}
когда r
близко к, вспомните, что
n
(обычно от 1 до 6) меньше
m
(обычно от 9 до 12), игнорируйте второй член, оцените вторую производную
( ∂ 2 ∂ r 2 u ) r = a 0 = − A n ( n + 1 ) r 0 − n − 2 {\displaystyle \left({\partial ^{2} \over \partial r^{2}}u\right)_{r=a_{0}}=-An(n+1)r_{0}^{-n-2}}
Напомним связь между r и Ω
Ω = 4 π 3 r 3 {\displaystyle \Omega ={4\pi \over 3}r^{3}} ( ∂ 2 ∂ Ω 2 u ) = ( ∂ 2 ∂ r 2 u ) ( ∂ r ∂ Ω ) 2 = ( ∂ 2 ∂ r 2 u ) Ω − 4 3 {\displaystyle \left({\partial ^{2} \over \partial \Omega ^{2}}u\right)=\left({\partial ^{2} \over \partial r^{2}}u\right)\left({\partial r \over \partial \Omega }\right)^{2}=\left({\partial ^{2} \over \partial r^{2}}u\right)\Omega ^{-{\frac {4}{3}}}} K = Ω 0 ( ∂ 2 u ∂ r 2 ) Ω = Ω 0 ∝ r 0 − n − 3 {\displaystyle K=\Omega _{0}\left({\partial ^{2}u \over \partial r^{2}}\right)_{\Omega =\Omega _{0}}\propto r_{0}^{-n-3}}
Во многих случаях, например, в металлических или ионных материалах, сила притяжения является электростатической, поэтому n
= 1, мы имеем
K ∝ r 0 − 4 {\displaystyle K\propto r_{0}^{-4}}
Это относится к атомам со схожей природой связи. Эта взаимосвязь подтверждается для щелочных металлов и многих ионных соединений. [6]
Ссылки [ править ]
- «Объемные упругие свойства» . гиперфизика
. Государственный университет Джорджии. - «Силиконовая резина» . Материалы AZO
. - Страница 52 из « Введение в физику твердого тела , 8-е издание» Чарльза Киттеля, 2005, ISBN 0-471-41526-X
- Флюгель, Александр. «Расчет объемного модуля стекол» . glassproperties.com
. - Х., Кортни, Томас (2013). Механическое поведение материалов
(2-е изд. Reimp ed.). Нью-Дели: McGraw Hill Education (Индия). ISBN 978-1259027512. OCLC 929663641 . - Перейти
↑ Gilman, JJ (1969).
Микромеханика течения в твердых телах
. Нью-Йорк: Макгроу-Хилл. п. 29.
Дальнейшее чтение [ править ]
- Де Йонг, Мартен; Чен, Вэй (2015). «Диаграмма полных упругих свойств неорганических кристаллических соединений» . Научные данные
.
2
: 150009. Bibcode : 2013NatSD … 2E0009D . DOI : 10.1038 / sdata.2015.9 . PMC 4432655 . PMID 25984348 .
| vтеМодули упругости для однородных изотропных материалов | |
| |
| Формулы преобразования | |||||||
| Однородные изотропные линейные упругие материалы обладают своими упругими свойствами, однозначно определяемыми любыми двумя модулями среди них; таким образом, для любых двух любых других модулей упругости можно рассчитать по этим формулам. | |||||||
| K = {\displaystyle K=\,} | E = {\displaystyle E=\,} | λ = {\displaystyle \lambda =\,} | G = {\displaystyle G=\,} | ν = {\displaystyle \nu =\,} | M = {\displaystyle M=\,} | Примечания | |
| ( K , E ) {\displaystyle (K,\,E)} | 3 K ( 3 K − E ) 9 K − E {\displaystyle {\tfrac {3K(3K-E)}{9K-E}}} | 3 K E 9 K − E {\displaystyle {\tfrac {3KE}{9K-E}}} | 3 K − E 6 K {\displaystyle {\tfrac {3K-E}{6K}}} | 3 K ( 3 K + E ) 9 K − E {\displaystyle {\tfrac {3K(3K+E)}{9K-E}}} | |||
| ( K , λ ) {\displaystyle (K,\,\lambda )} | 9 K ( K − λ ) 3 K − λ {\displaystyle {\tfrac {9K(K-\lambda )}{3K-\lambda }}} | 3 ( K − λ ) 2 {\displaystyle {\tfrac {3(K-\lambda )}{2}}} | λ 3 K − λ {\displaystyle {\tfrac {\lambda }{3K-\lambda }}} | 3 K − 2 λ {\displaystyle 3K-2\lambda \,} | |||
| ( K , G ) {\displaystyle (K,\,G)} | 9 K G 3 K + G {\displaystyle {\tfrac {9KG}{3K+G}}} | K − 2 G 3 {\displaystyle K-{\tfrac {2G}{3}}} | 3 K − 2 G 2 ( 3 K + G ) {\displaystyle {\tfrac {3K-2G}{2(3K+G)}}} | K + 4 G 3 {\displaystyle K+{\tfrac {4G}{3}}} | |||
| ( K , ν ) {\displaystyle (K,\,\nu )} | 3 K ( 1 − 2 ν ) {\displaystyle 3K(1-2\nu )\,} | 3 K ν 1 + ν {\displaystyle {\tfrac {3K\nu }{1+\nu }}} | 3 K ( 1 − 2 ν ) 2 ( 1 + ν ) {\displaystyle {\tfrac {3K(1-2\nu )}{2(1+\nu )}}} | 3 K ( 1 − ν ) 1 + ν {\displaystyle {\tfrac {3K(1-\nu )}{1+\nu }}} | |||
| ( K , M ) {\displaystyle (K,\,M)} | 9 K ( M − K ) 3 K + M {\displaystyle {\tfrac {9K(M-K)}{3K+M}}} | 3 K − M 2 {\displaystyle {\tfrac {3K-M}{2}}} | 3 ( M − K ) 4 {\displaystyle {\tfrac {3(M-K)}{4}}} | 3 K − M 3 K + M {\displaystyle {\tfrac {3K-M}{3K+M}}} | |||
| ( E , λ ) {\displaystyle (E,\,\lambda )} | E + 3 λ + R 6 {\displaystyle {\tfrac {E+3\lambda +R}{6}}} | E − 3 λ + R 4 {\displaystyle {\tfrac {E-3\lambda +R}{4}}} | 2 λ E + λ + R {\displaystyle {\tfrac {2\lambda }{E+\lambda +R}}} | E − λ + R 2 {\displaystyle {\tfrac {E-\lambda +R}{2}}} | R = E 2 + 9 λ 2 + 2 E λ {\displaystyle R={\sqrt {E^{2}+9\lambda ^{2}+2E\lambda }}} | ||
| ( E , G ) {\displaystyle (E,\,G)} | E G 3 ( 3 G − E ) {\displaystyle {\tfrac {EG}{3(3G-E)}}} | G ( E − 2 G ) 3 G − E {\displaystyle {\tfrac {G(E-2G)}{3G-E}}} | E 2 G − 1 {\displaystyle {\tfrac {E}{2G}}-1} | G ( 4 G − E ) 3 G − E {\displaystyle {\tfrac {G(4G-E)}{3G-E}}} | |||
| ( E , ν ) {\displaystyle (E,\,\nu )} | E 3 ( 1 − 2 ν ) {\displaystyle {\tfrac {E}{3(1-2\nu )}}} | E ν ( 1 + ν ) ( 1 − 2 ν ) {\displaystyle {\tfrac {E\nu }{(1+\nu )(1-2\nu )}}} | E 2 ( 1 + ν ) {\displaystyle {\tfrac {E}{2(1+\nu )}}} | E ( 1 − ν ) ( 1 + ν ) ( 1 − 2 ν ) {\displaystyle {\tfrac {E(1-\nu )}{(1+\nu )(1-2\nu )}}} | |||
| ( E , M ) {\displaystyle (E,\,M)} | 3 M − E + S 6 {\displaystyle {\tfrac {3M-E+S}{6}}} | M − E + S 4 {\displaystyle {\tfrac {M-E+S}{4}}} | 3 M + E − S 8 {\displaystyle {\tfrac {3M+E-S}{8}}} | E − M + S 4 M {\displaystyle {\tfrac {E-M+S}{4M}}} | S = ± E 2 + 9 M 2 − 10 E M {\displaystyle S=\pm {\sqrt {E^{2}+9M^{2}-10EM}}} Есть два верных решения. Знак плюс ведет к . ν ≥ 0 {\displaystyle \nu \geq 0} Знак минус ведет к . ν ≤ 0 {\displaystyle \nu \leq 0} | ||
| ( λ , G ) {\displaystyle (\lambda ,\,G)} | λ + 2 G 3 {\displaystyle \lambda +{\tfrac {2G}{3}}} | G ( 3 λ + 2 G ) λ + G {\displaystyle {\tfrac {G(3\lambda +2G)}{\lambda +G}}} | λ 2 ( λ + G ) {\displaystyle {\tfrac {\lambda }{2(\lambda +G)}}} | λ + 2 G {\displaystyle \lambda +2G\,} | |||
| ( λ , ν ) {\displaystyle (\lambda ,\,\nu )} | λ ( 1 + ν ) 3 ν {\displaystyle {\tfrac {\lambda (1+\nu )}{3\nu }}} | λ ( 1 + ν ) ( 1 − 2 ν ) ν {\displaystyle {\tfrac {\lambda (1+\nu )(1-2\nu )}{\nu }}} | λ ( 1 − 2 ν ) 2 ν {\displaystyle {\tfrac {\lambda (1-2\nu )}{2\nu }}} | λ ( 1 − ν ) ν {\displaystyle {\tfrac {\lambda (1-\nu )}{\nu }}} | Не может использоваться, когда ν = 0 ⇔ λ = 0 {\displaystyle \nu =0\Leftrightarrow \lambda =0} | ||
| ( λ , M ) {\displaystyle (\lambda ,\,M)} | M + 2 λ 3 {\displaystyle {\tfrac {M+2\lambda }{3}}} | ( M − λ ) ( M + 2 λ ) M + λ {\displaystyle {\tfrac {(M-\lambda )(M+2\lambda )}{M+\lambda }}} | M − λ 2 {\displaystyle {\tfrac {M-\lambda }{2}}} | λ M + λ {\displaystyle {\tfrac {\lambda }{M+\lambda }}} | |||
| ( G , ν ) {\displaystyle (G,\,\nu )} | 2 G ( 1 + ν ) 3 ( 1 − 2 ν ) {\displaystyle {\tfrac {2G(1+\nu )}{3(1-2\nu )}}} | 2 G ( 1 + ν ) {\displaystyle 2G(1+\nu )\,} | 2 G ν 1 − 2 ν {\displaystyle {\tfrac {2G\nu }{1-2\nu }}} | 2 G ( 1 − ν ) 1 − 2 ν {\displaystyle {\tfrac {2G(1-\nu )}{1-2\nu }}} | |||
| ( G , M ) {\displaystyle (G,\,M)} | M − 4 G 3 {\displaystyle M-{\tfrac {4G}{3}}} | G ( 3 M − 4 G ) M − G {\displaystyle {\tfrac {G(3M-4G)}{M-G}}} | M − 2 G {\displaystyle M-2G\,} | M − 2 G 2 M − 2 G {\displaystyle {\tfrac {M-2G}{2M-2G}}} | |||
| ( ν , M ) {\displaystyle (\nu ,\,M)} | M ( 1 + ν ) 3 ( 1 − ν ) {\displaystyle {\tfrac {M(1+\nu )}{3(1-\nu )}}} | M ( 1 + ν ) ( 1 − 2 ν ) 1 − ν {\displaystyle {\tfrac {M(1+\nu )(1-2\nu )}{1-\nu }}} | M ν 1 − ν {\displaystyle {\tfrac {M\nu }{1-\nu }}} | M ( 1 − 2 ν ) 2 ( 1 − ν ) {\displaystyle {\tfrac {M(1-2\nu )}{2(1-\nu )}}} | |||
Способы расчета модуля упругости
Известны также и другие характеристики упругости, которые описывают сопротивление материалов к воздействиям как к линейным, так и отличным от них.
Величина, которая характеризует сопротивление материала к растяжению, то есть увеличению его длины вдоль оси, или к сжатию – сокращению линейного размера, называется модулем продольной упругости.
Обозначается как Е и выражается в Па или ГПа.
Показывает зависимость относительного удлинения от нормальной составляющей cилы (F) к ее площади распространения (S) и упругости (Е):
σz = F/ES (3)
Параметр также называют модулем Юнга или модулем упругости первого рода, в таблице показаны величины для материалов различной природы.
| Название материала | Значение параметра, ГПа |
| Алюминий | 70 |
| Дюралюминий | 74 |
| Железо | 180 |
| Латунь | 95 |
| Медь | 110 |
| Никель | 210 |
| Олово | 35 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 190/210 |
| Стекло | 70 |
| Титан | 112 |
| Хром | 300 |
Модулем упругости второго рода называют модуль сдвига (G), который показывает сопротивление материала к сдвигающей силе (FG). Может быть выражена двумя способами.
- Через касательные напряжения (τz) и угол сдвига (γ):
G = τz/γ (4)
- Через соотношение модуля упругости первого рода и коэффициента Пуасонна (ν):
G = E/2(1+υ) (5)
Определенное в результате экспериментов значение сопротивления материала изгибу, называется модулем упругости при изгибе, и вычисляется следующим образом:
EИ = ((0,05-0,1)Fр— 0,2Fр)L2 / 4bh3(ƒ2-ƒ1) (6)
где Fр – разрушающая сила, Н;
L – расстояние между опорами, мм;
b, h – ширина и толщина образца, мм;
ƒ1, ƒ2– прогибы, образованные в результате нагрузки F1 и F2.
При равномерном давлении по всему объему на объект, возникает его сопротивление, называемое объемным модулем упругости или модулем сжатия (К). Выразить этот параметр можно, практически через все известные модули и коэффициент Пуассона.
Определение модуля упругости щебеночного основания
Параметры Ламе также используют для описания оценки прочности материала. Их два μ – модуль сдвига и λ. Они помогают учитывать все изменения внутри материала в трехмерном пространстве, тогда соотношения между нормальным напряжением и деформацией будет выглядеть следующим образом:
σ = 2με + λtrace(ε)I (7)
Оба параметра могут быть выражены из следующих соотношений:
λ = νE / (1+ν)(1-2ν) (8)
μ = E / 2(1+ν) (9)