Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.
Основные сведения
Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м 2 или в Па.
Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (10 12 Па)
Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.
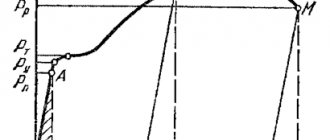
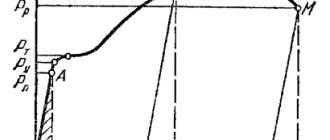
Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.
График теста на растяжение
E- это частное от деления нормальных напряжений σ на относительное удлинение ε.
Закон Гука также можно сформулировать и с использованием модуля Юнга.
Единица измерения и формулы
Единица измерения модуля Юнга в СИ — Ньютон на метр в квадрате (Н/м²), т.е. Паскаль (Па).
Формулы
Существует несколько формул, из которых можно вычислить модуль Юнга. Например, закон Гука.
Закон Гука
Можно вычислить модуль Юнга через эти формулы (мы это и сделаем на примере). Из-за этого закона существуют несколько интересных равенств, которые могут быть полезны для расчётов.
Закон Гука (этот описывает явления в теле, в дифференциальной форме):
Где:
- σ — механическое напряжение
- E — модуль Юнга (модуль упругости)
- ε — относительное удлинение
Закон Гука (этот описывает явления в теле)
Где:
- Fупр — сила упругости
- k × Δl — удлинение тела
Где:
- Fупр — сила упругости
- E — модуль Юнга (модуль упругости)
- S — площадь поперечного сечения
- l — первоначальная длина тела
- Δl — удлинение тела
Где:
- Fупр/S — механическое напряжение, обозначается как σ
- Δl/l — относительное удлинение, обозначается как ε
Следует заметить, что этот закон действует до той точки, когда материал необратимо деформируется и уже не возвращается в свою первоначальную форму. В какой точке это происходит, уже зависит от материала. Если материал очень жёсткий (значит высокое показание модуля упругости), то эта точка может совпадать с разрывом/деформацией.
Другие формулы вычисления модуля Юнга (модуля упругости)
Где:
- E — модуль Юнга (модуль упругости)
- k — жёсткость тела
- l — первоначальная длина стержня
- S — площадь поперечного сечения
Либо можно выразить k (жёсткость тела):
Где:
- k — жёсткость тела
- E — модуль Юнга (модуль упругости)
- S — площадь поперечного сечения
- l — первоначальная длина стержня/тела
Физический смысл модуля Юнга
Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.
Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.
Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.
В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:
Величину, обратную α, и называют модулем Юнга:
ε = (Δl) / l = α * (F/S)
Отношение растягивающей силы F к S называют упругим напряжением σ:
Закон Гука, записанный с использованием модуля Юнга, выглядит так:
Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.
В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.
Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l
Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.
Модуль упругости (модуль Юнга)
Содержание
- Модуль упругости Металлы
- Пластмассы
- Резины
- Дерево
- Минералы
- Различные материалы
Модуль упругости
Модуль упругости (модуль Юнга) E – характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к удлинению. Часто модуль Юнга называют просто модулем упругости.
1 кгс/мм2 = 10-6 кгс/м2 = 9,8·106 Н/м2 = 9,8·107 дин/см2 = 9,81·106 Па = 9,81 МПа
Модуль упругости (модуль Юнга)
| Материал | E | ||
| кгс/мм2 | 107 Н/м2 | МПа | |
| Металлы | |||
| Алюминий | 6300-7500 | 6180-7360 | 61800-73600 |
| Алюминий отожженный | 6980 | 6850 | 68500 |
| Бериллий | 30050 | 29500 | 295000 |
| Бронза | 10600 | 10400 | 104000 |
| Бронза алюминиевая, литье | 10500 | 10300 | 103000 |
| Бронза фосфористая катаная | 11520 | 11300 | 113000 |
| Ванадий | 13500 | 13250 | 132500 |
| Ванадий отожженный | 15080 | 14800 | 148000 |
| Висмут | 3200 | 3140 | 31400 |
| Висмут литой | 3250 | 3190 | 31900 |
| Вольфрам | 38100 | 37400 | 374000 |
| Вольфрам отожженный | 38800-40800 | 34200-40000 | 342000-400000 |
| Гафний | 14150 | 13900 | 139000 |
| Дюралюминий | 7000 | 6870 | 68700 |
| Дюралюминий катаный | 7140 | 7000 | 70000 |
| Железо кованое | 20000-22000 | 19620-21580 | 196200-215800 |
| Железо литое | 10200-13250 | 10000-13000 | 100000-130000 |
| Золото | 7000-8500 | 6870-8340 | 68700-83400 |
| Золото отожженное | 8200 | 8060 | 80600 |
| Инвар | 14000 | 13730 | 137300 |
| Индий | 5300 | 5200 | 52000 |
| Иридий | 5300 | 5200 | 52000 |
| Кадмий | 5300 | 5200 | 52000 |
| Кадмий литой | 5090 | 4990 | 49900 |
| Кобальт отожженный | 19980-21000 | 19600-20600 | 196000-206000 |
| Константан | 16600 | 16300 | 163000 |
| Латунь | 8000-10000 | 7850-9810 | 78500-98100 |
| Латунь корабельная катаная | 10000 | 9800 | 98000 |
| Латунь холоднотянутая | 9100-9890 | 8900-9700 | 89000-97000 |
| Магний | 4360 | 4280 | 42800 |
| Манганин | 12600 | 12360 | 123600 |
| Медь | 13120 | 12870 | 128700 |
| Медь деформированная | 11420 | 11200 | 112000 |
| Медь литая | 8360 | 8200 | 82000 |
| Медь прокатанная | 11000 | 10800 | 108000 |
| Медь холоднотянутая | 12950 | 12700 | 127000 |
| Молибден | 29150 | 28600 | 286000 |
| Нейзильбер | 11000 | 10790 | 107900 |
| Никель | 20000-22000 | 19620-21580 | 196200-215800 |
| Никель отожженный | 20600 | 20200 | 202000 |
| Ниобий | 9080 | 8910 | 89100 |
| Олово | 4000-5400 | 3920-5300 | 39200-53000 |
| Олово литое | 4140-5980 | 4060-5860 | 40600-58600 |
| Осмий | 56570 | 55500 | 555000 |
| Палладий | 10000-14000 | 9810-13730 | 98100-137300 |
| Палладий литой | 11520 | 11300 | 113000 |
| Платина | 17230 | 16900 | 169000 |
| Платина отожженная | 14980 | 14700 | 147000 |
| Родий отожженный | 28030 | 27500 | 275000 |
| Рутений отожженный | 43000 | 42200 | 422000 |
| Свинец | 1600 | 1570 | 15700 |
| Свинец литой | 1650 | 1620 | 16200 |
| Серебро | 8430 | 8270 | 82700 |
| Серебро отожженное | 8200 | 8050 | 80500 |
| Сталь инструментальная | 21000-22000 | 20600-21580 | 206000-215800 |
| Сталь легированная | 21000 | 20600 | 206000 |
| Сталь специальная | 22000-24000 | 21580-23540 | 215800-235400 |
| Сталь углеродистая | 19880-20900 | 19500-20500 | 195000-205000 |
| Стальное литье | 17330 | 17000 | 170000 |
| Тантал | 19000 | 18640 | 186400 |
| Тантал отожженный | 18960 | 18600 | 186000 |
| Титан | 11000 | 10800 | 108000 |
| Хром | 25000 | 24500 | 245000 |
| Цинк | 8000-10000 | 7850-9810 | 78500-98100 |
| Цинк катаный | 8360 | 8200 | 82000 |
| Цинк литой | 12950 | 12700 | 127000 |
| Цирконий | 8950 | 8780 | 87800 |
| Чугун | 7500-8500 | 7360-8340 | 73600-83400 |
| Чугун белый, серый | 11520-11830 | 11300-11600 | 113000-116000 |
| Чугун ковкий | 15290 | 15000 | 150000 |
| Пластмассы | |||
| Плексиглас | 535 | 525 | 5250 |
| Целлулоид | 173-194 | 170-190 | 1700-1900 |
| Стекло органическое | 300 | 295 | 2950 |
| Резины | |||
| Каучук | 0,80 | 0,79 | 7,9 |
| Резина мягкая вулканизированная | 0,15-0,51 | 0,15-0,50 | 1,5-5,0 |
| Дерево | |||
| Бамбук | 2000 | 1960 | 19600 |
| Береза | 1500 | 1470 | 14700 |
| Бук | 1600 | 1630 | 16300 |
| Дуб | 1600 | 1630 | 16300 |
| Ель | 900 | 880 | 8800 |
| Железное дерево | 2400 | 2350 | 32500 |
| Сосна | 900 | 880 | 8800 |
| Минералы | |||
| Кварц | 6800 | 6670 | 66700 |
| Различные материалы | |||
| Бетон | 1530-4100 | 1500-4000 | 15000-40000 |
| Гранит | 3570-5100 | 3500-5000 | 35000-50000 |
| Известняк плотный | 3570 | 3500 | 35000 |
| Кварцевая нить (плавленая) | 7440 | 7300 | 73000 |
| Кетгут | 300 | 295 | 2950 |
| Лед (при -2 °С) | 300 | 295 | 2950 |
| Мрамор | 3570-5100 | 3500-5000 | 35000-50000 |
| Стекло | 5000-7950 | 4900-7800 | 49000-78000 |
| Стекло крон | 7200 | 7060 | 70600 |
| Стекло флинт | 5500 | 5400 | 70600 |
Литература
- Краткий физико-технический справочник. Т.1 / Под общ. ред. К.П. Яковлева. М.: ФИЗМАТГИЗ. 1960. – 446 с.
- Справочник по сварке цветных металлов / С.М. Гуревич. Киев.: Наукова думка. 1981. 680 с.
- Справочник по элементарной физике / Н.Н. Кошкин, М.Г. Ширкевич. М., Наука. 1976. 256 с.
- Таблицы физических величин. Справочник / Под ред. И.К. Кикоина. М., Атомиздат. 1976, 1008 с.
Значения модуля юнга для некоторых материалов
В таблице показаны значения E ряда распространенных веществ.
| Материал | модуль Юнга E, ГПа |
| Алюминий | 70 |
| Бронза | 75-125 |
| Вольфрам | 350 |
| Графен | 1000 |
| Латунь | 95 |
| Лёд | 3 |
| Медь | 110 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 200/210 |
| Стекло | 70 |
Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.
Модуль Юнга (упругости)
Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.
Предел прочности материала
Это предел возникающего напряжения, после которого образец начинает разрушаться.
Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.
Читать также: Модель генератора переменного тока
Инструмент для определения предела прочности
Кроме того, существуют пределы прочности на сжатие материала и на растяжение. Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.
Допускаемое механическое напряжение в некоторых материалах при растяжении
Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.
Испытание на растяжение
Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.
| Материалы | σраст | |
| Бор | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловолокно | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
Запасы прочности, закладываемые в ответственные конструкции, также многократны.
Модуль упругости меди
Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой.
Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга.
В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.
Модуль Юнга
Модуль упругости — что это такое? Определение модуля упругости для материалов
Модуль упругости — это физическая величина, которая характеризует упругое поведение материала при приложении к нему внешней силы в конкретном направлении. Под упругим поведением материала подразумевается его деформация в упругой области.
История исследования упругости материалов
Физическая теория упругих тел и их поведения при действии внешних сил была подробно рассмотрена и изучена английским ученым XIX века Томасом Юнгом.
Однако сама концепция упругости была развита еще в 1727 году швейцарским математиком, физиком и философом Леонардом Эйлером, а первые эксперименты, связанные с модулем упругости, провел в 1782 году, то есть за 25 лет до работ Томаса Юнга, венецианский математик и философ Якопо Рикатти.
Заслуга Томаса Юнга заключается в том, что он придал теории упругости стройный современный вид, который впоследствии был оформлен в виде простого, а затем и обобщенного закона Гука.
Физическая природа упругости
Любое тело состоит из атомов, между которыми действуют силы притяжения и отталкивания. Равновесие этих сил обуславливает состояние и параметры вещества при данных условиях.
Атомы твердого тела при приложении к ним незначительных внешних сил растяжения или сжатия начинают смещаться, создавая противоположную по направлению и равную по модулю силу, которая стремится вернуть атомы в начальное состояние.
В процессе такого смещения атомов энергия всей системы увеличивается. Эксперименты показывают, что при малых деформациях энергия пропорциональна квадрату величины этих деформаций.
Это означает, что сила, будучи производной по энергии, оказывается пропорциональной первой степени величины деформации, то есть зависит от нее линейно.
Отвечая на вопрос, что такое модуль упругости, можно сказать, что это коэффициент пропорциональности между силой, действующей на атом, и деформацией, которую эта сила вызывает. Размерность модуля Юнга совпадает с размерностью давления (Паскаль).
Коэффициент запаса прочности
Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.
Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.
Связь с другими модулями упругости
Модуль Юнга связан с модулем сдвига, определяющим способность образца к сопротивлению против деформации сдвига, следующим соотношением:
E связан также и с модулем объёмной упругости, определяющим способность образца к сопротивлению против одновременного сжатия со всех сторон.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Одной из главных задач инженерного проектирования является выбор материала конструкции и оптимального сечения профиля. Необходимо найти тот размер, который при минимально возможной массе будет обеспечивать сохранение формы системы под воздействием нагрузки.
Например, какой номер стального двутавра использовать в качестве пролетной балки сооружения? Если взять профиль размерами ниже требуемого, то гарантировано получим разрушение строения. Если больше, то это ведет к нерациональному использованию металла, а, следовательно, утяжелению конструкции, усложнению монтажа, увеличению финансовых затрат. Знание такого понятия как модуль упругости стали даст ответ на вышепоставленный вопрос, и позволит избежать появления данных проблем на самом раннем этапе производства.
Как определить модуль упругости стали
Выяснить модули упругости для различных марок стали можно несколькими путями:
- по справочным данным из таблиц;
- экспериментальными методами для небольшого образца;
- расчетными методами, зная необходимые данные.
Жесткость стали зависит от ее химического состава и вида кристаллической решетки, от плотности, достигнутой в результате обработки. Прочность же ее конструкций определяется такими важными факторами, как параметры изделия, в том числе габариты, эксплуатационные нагрузки, и их длительность. При расчетах, выполняемых по нормированным методикам, результат осознанно завышают, чтобы предупредить возможные аварии и поломки.
Тем не менее, устойчивость стали к деформации определяется изначально ее маркой, то есть наличием примесей в сплаве.
В таблице приведены модули упругости стали наиболее популярных марок, а модуль сдвига ее составляет – 80-81 ГПа.
При расчете строительных конструкций нужно знать расчетное сопротивление и модуль упругости для того или иного материала. Здесь представлены данные по основным строительным материалам.
Таблица 1. Модули упругости для основных строительных материалов
Нормативные данные для рассчетов железобетонных конструкций
Таблица 2. Модули упругости бетона (согласно СП 52-101-2003)
Таблица 2.1 Модули упругости бетона согласно СНиП 2.03.01-84*(1996)
Примечания: 1. Над чертой указаны значения в МПа, под чертой — в кгс/см². 2. Для легкого, ячеистого и поризованного бетонов при промежуточных значениях плотности бетона начальные модули упругости принимают по линейной интерполяции. 3. Для ячеистого бетона неавтоклавного твердения значения Еb принимают как для бетона автоклавного твердения с умножением на коэффициент 0,8. 4. Для напрягающего бетона значения Еb принимают как для тяжелого бетона с умножением на коэффициент a
= 0,56 + 0,006В.
Таблица 3. Нормативные значения сопротивления бетона (согласно СП 52-101-2003)
Таблица 4. Расчетные значения сопротивления бетона сжатию (согласно СП 52-101-2003)
Таблица 4.1 Расчетные значения сопротивления бетона сжатию согласно СНиП 2.03.01-84*(1996)
Таблица 5. Расчетные значения сопротивления бетона растяжению (согласно СП 52-101-2003)
Таблица 6. Нормативные сопротивления для арматуры (согласно СП 52-101-2003)
Таблица 6.1 Нормативные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)
Таблица 6.2 Нормативные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)
Таблица 7. Расчетные сопротивления для арматуры (согласно СП 52-101-2003)
Таблица 7.1 Расчетные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)
Таблица 7.2 Расчетные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)
Нормативные данные для расчетов металлических контрукций
Таблица 8. Нормативные и расчетные сопротивления при растяжении, сжатии и изгибе (согласно СНиП II-23-81 (1990)) листового, широкополосного универсального и фасонного проката по ГОСТ 27772-88 для стальных конструкций зданий и сооружений
Примечания: 1. За толщину фасонного проката следует принимать толщину полки (минимальная его толщина 4 мм). 2. За нормативное сопротивление приняты нормативные значения предела текучести и временного сопротивления по ГОСТ 27772-88. 3. Значения расчетных сопротивлений получены делением нормативных сопротивлений на коэффициенты надежности по материалу, с округлением до 5 МПа (50 кгс/см²).
Таблица 9. Марки стали, заменяемые сталями по ГОСТ 27772-88 (согласно СНиП II-23-81 (1990))
Примечания: 1. Стали С345 и С375 категорий 1, 2, 3, 4 по ГОСТ 27772-88 заменяют стали категорий соответственно 6, 7 и 9, 12, 13 и 15 по ГОСТ 19281-73* и ГОСТ 19282-73*. 2. Стали С345К, С390, С390К, С440, С590, С590К по ГОСТ 27772-88 заменяют соответствующие марки стали категорий 1-15 по ГОСТ 19281-73* и ГОСТ 19282-73*, указанные в настоящей таблице. 3. Замена сталей по ГОСТ 27772-88 сталями, поставляемыми по другим государственным общесоюзным стандартам и техническим условиям, не предусмотрена.
Расчетные сопротивления для стали, используемой для производства профилированных листов здесь не показаны.
Общее понятие
Модуль упругости (также известный как модуль Юнга) – один из показателей механических свойств материала, который характеризует его сопротивляемость деформации растяжения. Другими словами, его значение показывает пластичность материала. Чем больше модуль упругости, тем менее будет растягиваться какой-либо стержень при прочих равных условиях (величина нагрузки, площадь сечения и прочее).
В теории упругости модуль Юнга обозначается буквой Е. Является составной частью закона Гука (закона о деформации упругих тел). Связывает напряжение, возникающее в материале, и его деформацию.
Согласно международной стандартной системе единиц измеряется в МПа. Но на практике инженеры предпочитают использовать размерность кгс/см2.
Определение модуля упругости осуществляется опытным путем в научных лабораториях. Суть данного способа заключается в разрыве на специальном оборудовании гантелеобразных образцов материала. Узнав напряжение и удлинение, при котором произошло разрушение образца, делят данные переменные друг на друга, тем самым получая модуль Юнга.
Отметим сразу, что таким методом определяются модули упругости пластичных материалов: сталь, медь и прочее. Хрупкие материалы – чугун, бетон – сжимают до появления трещин.
Дополнительные характеристики механических свойств
Модуль упругости дает возможность предугадать поведение материла только при работе на сжатие или растяжение. При наличии таких видов нагрузок как смятие, срез, изгиб и прочее потребуется введение дополнительных параметров:
- Жесткость есть произведение модуля упругости на площадь поперечного сечения профиля. По величине жесткости можно судить о пластичности уже не материала, а узла конструкции в целом. Измеряется в килограммах силы.
- Относительное продольное удлинение показывает отношение абсолютного удлинения образца к общей длине образца. Например, к стержню длиной 100 мм приложили определенную силу. Как результат, он уменьшился в размере на 5 мм. Деля его удлинение (5 мм) на первоначальную длину (100 мм) получаем относительное удлинение 0,05. Переменная является безразмерной величиной. В некоторых случаях для удобства восприятия переводится в проценты.
- Относительное поперечное удлинение рассчитывается аналогично вышепредставленному пункту, но вместо длины здесь рассматривается диаметр стержня. Опыты показывают, что для большинства материалов поперечное удлинение в 3-4 раза меньше, чем продольное.
- Коэффициент Пуансона есть отношение относительной продольной деформации к относительной поперечной деформации. Данный параметр позволяет полностью описать изменение формы под воздействием нагрузки.
- Модуль сдвига характеризует упругие свойства при воздействии на образец касательных напряжений, т. е. в случае, когда вектор силы направлен под 90 градусов к поверхности тела. Примерами таких нагрузок является работа заклепок на срез, гвоздей на смятие и прочее. По большому счету, модуль сдвига связан с таким понятием как вязкость материла.
- Модуль объемной упругости характеризуется изменением объема материала для равномерного разностороннего приложения нагрузки. Является отношением объемного давления к объемной деформации сжатия. Примером такой работы служит опущенный в воду образец, на который по всей его площади воздействует давление жидкости.
Читать также: Принцип работы двухтактного дизеля
Помимо вышесказанного необходимо упомянуть, что некоторые типы материалов имеют различные механические свойства в зависимости от направления нагрузки. Такие материалы характеризуются как анизотропные. Яркими примерами служит древесина, слоистые пластмассы, некоторые виды камня, ткани и прочее.
У изотропных материалов механические свойства и упругая деформация одинаковы в любом направлении. К ним относят металлы (сталь, чугун, медь, алюминий и прочее), неслоистые пластмассы, естественные камни, бетон, каучук.
От чего зависит модуль упругости бетона?
Упругие свойства бетона зависят от факторов:
- качества и объемного содержания заполнителей;
- класса материала;
- температуры воздуха и интенсивности радиоактивного излучения;
- влажности среды;
- времени воздействия нагрузки;
- условий твердения смеси;
- возраста бетона;
- армирования.
Заполнители
Бетон представляет собой конгломерат из двух составляющих — цементного камня и заполнителей. В неоднородной структуре возникает сложное напряженное состояние. Более жесткие частицы воспринимают основную часть нагрузки, а вокруг пор и пустот образуются участки с поперечными растягивающими усилиями.
Крупный заполнитель, обладая высоким модулем Юнга, увеличивает упругие свойства бетона. Мелкие пылеватые частицы, поры и пустоты снижают их.
Класс бетона
Чем выше класс материала, т.е. больше его прочность на сжатие и плотность, тем лучше он сопротивляется деформирующим нагрузкам. Наиболее высоким модулем упругости обладает бетон В60 — 39,5 МПа*10-3, минимальный показатель у композита класса В10- 19 МПа*10-3.
Температура и радиация
Повышение температуры окружающей среды, интенсивности солнечной радиации приводят к уменьшению упругих свойств и росту деформаций. Связано это с увеличением внутренней энергии бетона, изменению траекторий движения молекул в твердом теле, линейному расширению материала, и, как следствию, усилению пластичности.
Разницу не учитывают при колебаниях в пределах 20°С. Большие температурные изменения существенно влияют на деформацию бетонных конструкций. В таблице СП 63.13330.2012 указаны величины модулей упругости в зависимости от температуры.
Влажность
Колебания влажности воздуха приводят к изменению упругих свойств материала. В расчетах применяют коэффициент ползучести φ. Чем больше содержание водяных паров в окружающей среде, тем ниже показатель и соответственно меньше пластические деформации конструкции.
Время приложения нагрузки
Модуль упругости зависит от времени действия нагрузки. При мгновенном нагружении конструкции деформации пропорциональны величине внешних сил. При длительных напряжениях величина E уменьшается, изменения развиваются по нелинейной зависимости и суммируются из упругих и пластичных деформаций.
Условия набора прочности
При проведении испытаний замечено, что у бетона естественного твердения модуль упругости выше, чем при обработке материала пропариванием при атмосферном давлении или в автоклавных установках.
Это объясняется тем, что изменение условий набора прочности приводит к образованию большего количества пор и пустот из-за неравномерного температурного расширения объема, ухудшения качества гидратации цементных зерен. Такой бетон обладает более низкими упругими свойствами по сравнению с затвердевшим в нормальных условиях.
Возраст бетона
Свежеуложенный бетон набирает прочность в течение 28 суток. Но даже по истечении этого времени материал при нагрузке обладает одновременно упругими и пластическими свойствами. Наибольшей твердости он достигает примерно через 200-250 суток. Показатель E в этом возрасте максимальный, соответствующий марочной прочности.
Армирование конструкций
Для восприятия растягивающих и сжимающих усилий в железобетон помещают каркасы или сетки из арматуры классов АI, AIII, А500С, Ат800, а также из композитов или древесины.
Применение армирования увеличивает упругость, прочность конструкции на сжатие и на растяжение при изгибе, препятствует образованию усадочных и деформационных трещин.
Значение модуля упругости
Необходимо заметить, что модуль Юнга не является постоянной величиной. Даже для одного и того же материала он может колебаться в зависимости от точек приложения силы.
Некоторые упруго – пластичные материалы обладают более или менее постоянным модулем упругости при работе как на сжатие, так и на растяжение: медь, алюминий, сталь. В других случаях упругость может изменяться исходя из формы профиля.
Вот примеры значений модуля Юнга (в миллионах кгссм2) некоторых материалов:
- Чугун белый – 1,15.
- Чугун серый -1,16.
- Латунь – 1,01.
- Бронза – 1,00.
- Кирпичная каменная кладка – 0,03.
- Гранитная каменная кладка – 0,09.
- Бетон – 0,02.
- Древесина вдоль волокон – 0,1.
- Древесина поперек волокон – 0,005.
- Алюминий – 0,7.
Рассмотрим разницу в показаниях между модулями упругости для сталей в зависимости от марки:
- Стали конструкционные высокого качества (20, 45) – 2,01.
- Стали обычного качества (Ст.3, Ст.6) – 2,00.
- Стали низколегированные (30ХГСА, 40Х) – 2,05.
- Стали нержавеющие (12Х18Н10Т) – 2,1.
- Стали штамповые (9ХМФ) – 2,03.
- Стали пружинные (60С2) – 2,03.
- Стали подшипниковые (ШХ15) – 2,1.
Также значение модуля упругости для сталей изменяется исходя из вида проката:
- Проволока высокой прочности – 2,1.
- Плетенный канат – 1,9.
- Трос с металлическим сердечником – 1,95.
Как видим, отклонения между сталями в значениях модулей упругой деформации имеют небольшую величину. Поэтому в большинстве инженерных расчетов можно пренебречь погрешностями и брать значение Е=2,0.
Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.
Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними. Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда. С повышением прочностных характеристик совершенствовались инструменты и способы производства.
Модуль упругости различных материалов
Модули упругости для различных материалов имеют совершенно разные значения, которые зависят от:
- природы веществ, формирующих состав материала;
- моно- или многокомпонентный состав (чистое вещество, сплав и так далее);
- структуры (металлическая или другой вид кристаллической решетки, молекулярное строение прочее);
- плотности материала (распределения частиц в его объеме);
- обработки, которой он подвергался (обжиг, травление, прессование и тому подобное).
Так, например, в справочных данных можно найти, что модуль упругости для алюминия составляет диапазон от 61,8 до 73,6 ГПа. Видимо, это и зависит от состояния металла и вида обработки, потому как для отожженного алюминия модуль Юнга – 68,5 ГПа.
Его значение для бронзовых материалов зависит не только от обработки, но и от химического состава:
- бронза – 10,4 ГПа;
- алюминиевая бронза при литье – 10,3 ГПа;
- фосфористая бронза катанная – 11,3 ГПа.
Модуль Юнга латуни на много ниже – 78,5-98,1. Максимальное значение имеет катанная латунь.
Сама же медь в чистом виде характеризуется сопротивлением к внешним воздействиям значительно большим, чем ее сплавы – 128,7 ГПа. Обработка ее также снижает показатель, в том числе и прокатка:
- литая – 82 ГПа;
- прокатанная – 108 ГПа;
- деформированная – 112 ГПа;
- холоднотянутая – 127 ГПа.
Близким значением к меди обладает титан (108 ГПа), который считается одним из самых прочных металлов. А вот тяжелый, но ломкий свинец, показывает всего 15,7-16,2 ГПа, что сравнимо с прочностью древесины.
Для железа показатель напряжения к деформации также зависит от метода его обработки: литое – 100-130 или кованное – 196,2-215,8 ГПа.
Чугун известен своей хрупкостью имеет отношение напряжения к деформации от 73,6 до 150 ГПа, что соответствует от его виду. Тогда как для стали модуль упругости может достигать 235 ГПа.
На величины параметров прочности влияют также и формы изделий. Например, для стального каната проводят расчеты, где учитывают:
Интересно, что этот показатель для каната будет значительно ниже, чем для проволоки такого же диаметра.
Стоит отметить прочность и не металлических материалов. Например, среди модулей Юнга дерева наименьший у сосны – 8,8 ГПа, а вот у группы твердых пород, которые объединены под названием «железное дерево» самый высокий – 32,5 ГПа, дуб и бук имеют равные показатели – 16,3 ГПа.
Среди строительных материалов, сопротивление к внешним силам у, казалось бы, прочного гранита всего 35-50 ГПа, когда даже у стекла – 78 ГПа. Уступают стеклу бетон – до 40 ГПа, известняк и мрамор, со значениями 35 и 50 ГПа соответственно.
Такие гибкие материалы, как каучук и резина, выдерживают осевую нагрузку от 0,0015 до 0,0079 ГПа.
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
- Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.
Читать также: Схема плавного пуска пылесоса
- Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.
- Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
- Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
- Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.
Понятие о модуле упругости
В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
- Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
- Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).
Формула по закону Гука записывается в виде ε = σz/E, где:
- ε – относительное удлинение;
- σz – нормальное напряжение.
Демонстрация закона Гука для упругих тел:
Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.
В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.
Значения модуля упругости для некоторых материалов приведены в таблице 1.
Таблица 1: Модуль упругости для металлов и сплавов
| Наименование материала | Значение модуля упругости, 10¹²·Па |
| Алюминий | 65…72 |
| Дюралюминий | 69…76 |
| Железо, содержание углерода менее 0,08 % | 165…186 |
| Латунь | 88…99 |
| Медь (Cu, 99 %) | 107…110 |
| Никель | 200…210 |
| Олово | 32…38 |
| Свинец | 14…19 |
| Серебро | 78…84 |
| Серый чугун | 110…130 |
| Сталь | 190…210 |
| Стекло | 65…72 |
| Титан | 112…120 |
| Хром | 300…310 |
Способы расчета модуля упругости
Известны также и другие характеристики упругости, которые описывают сопротивление материалов к воздействиям как к линейным, так и отличным от них.
Обозначается как Е и выражается в Па или ГПа.
Показывает зависимость относительного удлинения от нормальной составляющей cилы (F) к ее площади распространения (S) и упругости (Е):
σz = F/ES (3)
Параметр также называют модулем Юнга или модулем упругости первого рода, в таблице показаны величины для материалов различной природы.
| Название материала | Значение параметра, ГПа |
| Алюминий | 70 |
| Дюралюминий | 74 |
| Железо | 180 |
| Латунь | 95 |
| Медь | 110 |
| Никель | 210 |
| Олово | 35 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 190/210 |
| Стекло | 70 |
| Титан | 112 |
| Хром | 300 |
Модулем упругости второго рода называют модуль сдвига (G), который показывает сопротивление материала к сдвигающей силе (FG). Может быть выражена двумя способами.
Через касательные напряжения (τz) и угол сдвига (γ):
G = τz/γ (4)
Через соотношение модуля упругости первого рода и коэффициента Пуасонна (ν):
G = E/2(1+υ) (5)
Определенное в результате экспериментов значение сопротивления материала изгибу, называется модулем упругости при изгибе, и вычисляется следующим образом:
EИ = ((0,05-0,1)Fр— 0,2Fр)L2 / 4bh3(ƒ2-ƒ1) (6)
где Fр – разрушающая сила, Н;
L – расстояние между опорами, мм;
b, h – ширина и толщина образца, мм;
ƒ1, ƒ2– прогибы, образованные в результате нагрузки F1 и F2.
При равномерном давлении по всему объему на объект, возникает его сопротивление, называемое объемным модулем упругости или модулем сжатия (К). Выразить этот параметр можно, практически через все известные модули и коэффициент Пуассона.
Определение модуля упругости щебеночного основания
Параметры Ламе также используют для описания оценки прочности материала. Их два μ – модуль сдвига и λ. Они помогают учитывать все изменения внутри материала в трехмерном пространстве, тогда соотношения между нормальным напряжением и деформацией будет выглядеть следующим образом:
σ = 2με + λtrace(ε)I (7)
Оба параметра могут быть выражены из следующих соотношений:
λ = νE / (1+ν)(1-2ν) (8)
μ = E / 2(1+ν) (9)
Модуль упругости для разных марок стали
Металлурги разработали несколько сотен марок сталей. Им свойственны разные значения прочности. В таблице 2 показаны характеристики для наиболее распространенных сталей.
Таблица 2: Упругость сталей
| Наименование стали | Значение модуля упругости, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 |
| Сталь 3 | 179…189 |
| Сталь 30 | 194…205 |
| Сталь 45 | 211…223 |
| Сталь 40Х | 240…260 |
| 65Г | 235…275 |
| Х12МФ | 310…320 |
| 9ХС, ХВГ | 275…302 |
| 4Х5МФС | 305…315 |
| 3Х3М3Ф | 285…310 |
| Р6М5 | 305…320 |
| Р9 | 320…330 |
| Р18 | 325…340 |
| Р12МФ5 | 297…310 |
| У7, У8 | 302…315 |
| У9, У10 | 320…330 |
| У11 | 325…340 |
| У12, У13 | 310…315 |
Видео: закон Гука, модуль упругости.
Модули прочности
Кроме нормального нагружения, существуют и иные силовые воздействия на материалы.
Модуль сдвига G определяет жесткость. Эта характеристика показывает предельное значение нагрузки изменению формы предмета.
Модуль объемной упругости К определяет упругие свойства материала изменить объем. При любой деформации происходит изменение формы предмета.
Для разных сталей значения указанных модулей приведены в таблице 3.
Таблица 3: Модули прочности для сталей
| Наименование стали | Модуль упругости Юнга, 10¹²·Па | Модуль сдвига G, 10¹²·Па | Модуль объемной упругости, 10¹²·Па | Коэффициент Пуассона, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 | 87…91 | 45…49 | 154…168 |
| Сталь 3 | 179…189 | 93…102 | 49…52 | 164…172 |
| Сталь 30 | 194…205 | 105…108 | 72…77 | 182…184 |
| Сталь 45 | 211…223 | 115…130 | 76…81 | 192…197 |
| Сталь 40Х | 240…260 | 118…125 | 84…87 | 210…218 |
| 65Г | 235…275 | 112…124 | 81…85 | 208…214 |
| Х12МФ | 310…320 | 143…150 | 94…98 | 285…290 |
| 9ХС, ХВГ | 275…302 | 135…145 | 87…92 | 264…270 |
| 4Х5МФС | 305…315 | 147…160 | 96…100 | 291…295 |
| 3Х3М3Ф | 285…310 | 135…150 | 92…97 | 268…273 |
| Р6М5 | 305…320 | 147…151 | 98…102 | 294…300 |
| Р9 | 320…330 | 155…162 | 104…110 | 301…312 |
| Р18 | 325…340 | 140…149 | 105…108 | 308…318 |
| Р12МФ5 | 297…310 | 147…152 | 98…102 | 276…280 |
| У7, У8 | 302…315 | 154…160 | 100…106 | 286…294 |
| У9, У10 | 320…330 | 160…165 | 104…112 | 305…311 |
| У11 | 325…340 | 162…170 | 98…104 | 306…314 |
| У12, У13 | 310…315 | 155…160 | 99…106 | 298…304 |
Для других материалов значения прочностных характеристик указывают в специальной литературе. Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.
Модуль упругости меди — Справочник металлиста
Основной главной задачей инженерного проектирования служит выбор оптимального сечения профиля и материала конструкции. Нужно найти именно тот размер, который обеспечит сохранение формы системы при минимальной возможной массе под влиянием нагрузки.
К примеру, какую именно сталь следует применять в качестве пролётной балки сооружения? Материал может использоваться нерационально, усложнится монтаж и утяжелится конструкция, увеличатся финансовые затраты. На этот вопрос ответит такое понятие как модуль упругости стали.
Он же позволит на самой ранней стадии избежать появления этих проблем.
- Общие понятия
- Механические свойства
- Модуль упругости
Модуль упругости (модуль Юнга) — это показатель механического свойства материала, характеризующий его сопротивляемость деформации растяжения. Иными словами, это значение пластичности материала. Чем выше значения модуля упругости, тем меньше будет какой-либо стержень растягиваться при иных равных нагрузках (площадь сечения, величина нагрузки и другие).
Модуль Юнга в теории упругости обозначается буквой Е. Он является составляющей закона Гука (о деформации упругих тел). Эта величина связывает возникающее в образце напряжение и его деформацию.
Измеряется эта величина согласно стандартной международной системе единиц в МПа (Мегапаскалях). Но инженеры на практике больше склоняются к применению размерности кгс/см2.
Опытным путём осуществляется определение этого показателя в научных лабораториях. Сутью этого метода является разрыв гантелеобразных образцов материала на специальном оборудовании. Узнав удлинение и натяжение, при которых образец разрушился, делят переменные данные друг на друга. Полученная величина и является модулем (Юнга) упругости.
Таким образом определяется только модуль Юнга материалов упругих: медь, сталь и прочее. А материалы хрупкие сжимают до того момента, пока не появятся трещины: бетон, чугун и им подобные.
Механические свойства
Только при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала. А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры:
- Жёсткостью называют произведение поперечного сечения профиля на модуль упругости. По этой величине можно судить о пластичности узла конструкции в целом, а не о материале отдельно. Единицей измерения являются килограммы силы.
- Продольное относительное удлинение — это отношение абсолютного удлинения материала-образца к его общей длине. К примеру, на стержень, длина которого равна 200 миллиметров, приложили некоторую силу. В результате он стал короче на 5 миллиметров. В результате относительное удлинение будет равняться 0,05. Эта величина безразмерная. Для более удобного восприятия иногда её переводят в проценты.
- Поперечное относительное удлинение рассчитывается точно так же, как и продольное относительное удлинение, но вместо длины берут диаметр стержня. Опытным путём было установлено, что для большего количества материала поперечное меньше продольного удлинения приблизительно в 4 раза.
- Коэффициент Пуассона. Это отношения относительной продольной к относительной поперечной деформации. При помощи этой величины можно полностью описать под воздействием нагрузки изменения формы.
- Модуль сдвига описывает упругие свойства под воздействием касательных свойств на образец. Иными словами, когда вектор силы направляется к поверхности тела под 90 градусов. Примером подобных нагрузок служит работа гвоздей на смятие, заклёпок на срез и пр. Этот параметр связан с вязкостью материала.
- Модуль упругости объёмной характеризует изменение объёма образца для разностороннего равномерного приложения нагрузки. Эта величина является отношением давления объёмного к деформации сжатия объёмной. Как пример можно рассматривать опущенный в воду материал, на который воздействует давление жидкости по всей его площади.
Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства. Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.
У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.
Модуль упругости
Стоит отметить, что эта величина непостоянная. Даже для одного материала она может иметь разное значение в зависимости от того, в какие точки была приложена сила.
Кое-какие пластично-упругие материалы имеют практически постоянное значение модуля упругости при работе как на растяжение, так и на сжатие: сталь, алюминий, медь.
А есть и такие ситуации, когда эта величина измеряется формой профиля.