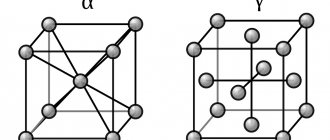
Кубическая гранецентрированная решетка: координационное число, структура и геометрия

Решетки Браве

Три решетки Браве в кубической кристаллической системе:

Решетка Браве	Примитивная кубическая	Телоцентрированный кубический	Гранецентрированная кубическая
Символ Пирсона	cP	cI	cF

Примитивная кубическая система (cP) состоит из одной точки решетки на каждом углу куба. Затем каждый атом в точке решетки поровну делится между восемью соседними кубами, и поэтому элементарная ячейка содержит всего один атом ( 1 ⁄ 8 × 8).

Объемно-центрированная кубическая система (cI) имеет одну точку решетки в центре элементарной ячейки в дополнение к восьми угловым точкам. Он имеет в сумме 2 точки решетки на элементарную ячейку ( 1 ⁄ 8 × 8 + 1).

Гранецентрированная кубическая система (cF) имеет точки решетки на гранях куба, каждая из которых дает ровно половину вклада в дополнение к угловым точкам решетки, что дает в общей сложности 4 точки решетки на элементарную ячейку ( 1 ⁄ 8 × 8 от углов плюс 1 ⁄ 2 × 6 от граней). Каждая сфера в решетке cF имеет координационное число 12. Координационное число – это число ближайших соседей центрального атома в структуре.

Гранецентрированная кубическая система тесно связана с гексагональной плотноупакованной (ГПУ) системой, где две системы различаются только относительным расположением своих гексагональных слоев. плоскость гранецентрированной кубической системы является шестиугольной сеткой.

Попытка создать C-центрированную кубическую кристаллическую систему (т.е. размещение дополнительной точки решетки в центре каждой горизонтальной грани) приведет к простой тетрагональной решетке Браве .

Примеры материалов

Все металлы характеризуются кристаллическим строением. Они отличаются наличием малоподвижных ионов с положительным зарядом и движущимися между ними электронами. Данные структуры именуют металлическими связями.

Объемно-центрированная кубическая решетка свойственна для Fe при комнатной температуре, W, V, Cr, Mo и прочих металлов.

Гранецентрированная кубическая решетка встречается на Mg, Ti, Zn, Zr и прочих металлах.

Дефекты кристаллического строения металлов

Однако все рассмотренные типы ячеек могут иметь и естественные недостатки, или так называемые дефекты. Это может быть связано с разными причинами: посторонними атомами и примесями в металлах, внешними воздействиями и прочим.

Поэтому существует классификация, отражающая дефекты, которые могут иметь кристаллические решетки. Химия как наука изучает каждый из них с целью выявления причины и способа устранения, чтобы свойства материала не были изменены. Итак, дефекты следующие.

Точечные. Они бывают трех основных видов: вакансии, примеси или дислоцированные атомы. Приводят к ухудшению магнитных свойств металла, электро- и теплопроводности его.
Линейные, или дислокационные. Выделяют краевые и винтовые. Ухудшают прочность и качество материала.
Поверхностные дефекты. Влияют на внешний вид и структуру металлов.

В настоящее время разработаны методики устранения дефектов и получения чистых кристаллов. Однако совсем искоренить их не удается, идеальной кристаллической решетки не существует.

Признаки

Все 14 видов элементарных ячеек обладают общими свойствами:

они являются простейшими повторяющимися структурами в кристалле;
каждый центр решетки состоит из одной частицы, называемый узлом решетки;
узлы ячейки соединяются между собой прямыми, которые формируют геометрию кристалла;
противоположные грани параллельны;
симметрия элементарной структуры соответствует симметрии всей кристаллической решетки.

При выборе структуры элементарной ячейки руководствуются некоторыми правилами. У нее должны быть:

наименьший объем и площадь;
наибольшее количество одинаковых ребер и углов между ними;
прямые углы (по возможности);
пространственная симметрия, отражающая симметрию всей кристаллической решетки.

Значение знаний о кристаллическом строении металлов

Из вышеизложенного материала очевидно, что знания о тонкой структуре и строении позволяют спрогнозировать свойства материала и повлиять на них. И это позволяет делать наука химия

9 класс общеобразовательной школы делает в процессе обучения упор на то, чтобы сформировать у учащихся четкое понятие о важном значении основополагающей логической цепочки: состав — строение — свойства — применение

Сведения о кристаллическом строении металлов очень четко иллюстрирует эту зависимость и позволяет учителю наглядно объяснить и показать детям, насколько важно знать тонкую структуру, чтобы правильно и грамотно использовать все свойства

Периодическая таблица и металлы

В XIX веке благодаря своему блестящему уму и многим годам труда Дмитрий Иванович Менделеев составил таблицу, собрав в нее все известные на то время химические элементы. Каждому из них в таблице отведено определенное положение в соответствии с числом протонов в атомном ядре. Вся таблица делится на 7 периодов (горизонтальные строки) и 8 групп (вертикальные строки). Чем больше период, тем больше радиус атома соответствующего элемента, и тем на более высоких орбиталях расположены его валентные электроны. Наоборот, чем старше группа (движение по таблице слева направо), тем больше валентных электронов находится на последней орбитали и тем меньше радиус атома.

Любой элемент таблицы можно условно отнести либо к металлам, либо к неметаллам. Металлы расположены по левую сторону от диагонали бор (B) – полоний (Po). Если взглянуть на таблицу, то можно сразу понять, что количество металлов в несколько раз превышает число неметаллов.

Читать также: Самодельный вискозиметр для краски

Полиморфизм

Кварц – одна из нескольких кристаллических форм кремнезема SiO 2 . Наиболее важные формы кремнезема включают: α-кварц , β-кварц , тридимит , кристобалит , коэсит и стишовит .

Полиморфизм – это появление нескольких кристаллических форм материала. Он содержится во многих кристаллических материалах, включая полимеры , минералы и металлы . Согласно правилам фазового равновесия Гиббса, эти уникальные кристаллические фазы зависят от интенсивных переменных, таких как давление и температура. Полиморфизм связан с аллотропией , которая относится к элементарным твердым телам . Полная морфология материала описывается полиморфизмом и другими переменными, такими как габитус кристаллов , аморфная фракция или кристаллографические дефекты . Полиморфы обладают разной стабильностью и могут спонтанно и необратимо превращаться из метастабильной формы (или термодинамически нестабильной формы) в стабильную форму при определенной температуре. Они также имеют разные температуры плавления , растворимость и дифрактограммы рентгеновских лучей .

Хорошим примером этого является кварцевая форма диоксида кремния или SiO 2 . В подавляющем большинстве силикатов атом Si имеет тетраэдрическую координацию по 4 атомам кислорода. Все кристаллические формы, кроме одной, включают тетраэдрические звенья {SiO 4 }, связанные вместе общими вершинами в разном расположении. В разных минералах тетраэдры демонстрируют разную степень сетки и полимеризации. Например, они встречаются поодиночке, соединены вместе попарно, в более крупные конечные кластеры, включая кольца, цепочки, двойные цепи, листы и трехмерные каркасы. Минералы классифицируются на группы на основе этих структур. В каждой из 7 термодинамически стабильных кристаллических форм или полиморфов кристаллического кварца только 2 из 4 ребер тетраэдров {SiO 4 } являются общими с другими, что дает чистую химическую формулу кремнезема: SiO 2 .

Другой пример – элементарное олово (Sn), которое является пластичным при температурах окружающей среды, но хрупким при охлаждении. Это изменение механических свойств связано с существованием двух его основных аллотропов , α- и β-олова. Два аллотропа , встречающиеся при нормальном давлении и температуре, α-олово и β-олово, более известны как серое олово

и
белое олово
соответственно. Еще два аллотропа, γ и σ, существуют при температурах выше 161 ° C и давлениях выше нескольких ГПа. Белое олово является металлическим и представляет собой стабильную кристаллическую форму при комнатной температуре или выше. При температуре ниже 13,2 ° C олово существует в серой форме, имеющей кубическую кристаллическую структуру алмаза , подобную алмазу , кремнию или германию . Серое олово вообще не имеет металлических свойств, представляет собой тускло-серый порошкообразный материал и имеет несколько применений, кроме нескольких специализированных полупроводниковых применений. Хотя температура α – β превращения олова номинально составляет 13,2 ° C, примеси (например, Al, Zn и т. Д.) Понижают температуру перехода значительно ниже 0 ° C, и при добавлении Sb или Bi превращение может вообще не происходить.

Элементарная ячейка. Кристаллические решетки.

Ограничивающие кристалл плоскости, или грани, имеют вполне определенное отношение к его структуре, организующей атомы в единую систему. Внутренняя структурная решетка состоит из ячеек, каждая из которых представляет собой группу связанных друг с другом атомов (или ионов), расположенных в пространстве строго фик-

сированно. Эти мельчайшие ячейки, повторяясь в трех измерениях, образуют кристалл. Они называются элементарными ячейками структуры.

Представление об элементарной ячейке легче всего проиллюстрировать на примере двумерного рисунка, скажем такого, какой могут иметь обои. На рис. 3.3 приведен пример двумерной решетки, несколько возможных элементарных ячеек которой обведены жирной линией.

3.1.2 Кристаллические решетки

Вершины ячеек представляют собой точки с идентичным окружением в любом заданном направлении. Конечно, без труда можно выбрать разные вершинные точки (например, на рис. 3.3: abdc, efhg, kjlm и т.д.), но чтобы удовлетворить требования, предъявляемые к элементарной ячейке, они должны иметь идентичное окружение по одинаковым направлениям. Такое пространственное расположение точек называется кристаллической решеткой. Двумерную решетку иногда называют плоской, чтобы отличить ее от трехмерной.

Если мы хотим определить структурную решетку кристалла, то для этого нужно прежде всего установить размеры (длины ребер) и углы между ребрами в выбранной элементарной ячейке. Обычно это наименьшая из ячеек, которую удается выбрать при условии согласия с проявляемой кристаллом полной симметрией. Длины ребер и углы между ними называются параметрами решетки. Помимо этого мы должны установить состав элементарной ячейки с точки зрения атомов или групп атомов химических элементов, слагающих данное вещество. Места их расположения определяются координатными осями, направленными вдоль ребер ячейки. В качестве примера на рис 3.4 приведена одна из элементарных ячеек решетки, представленной на рис. 3.3.

При рассмотрении всего круга кристаллических веществ становится очевидным, что размеры ребер и углы между ними могут быть бесконечно разнообразными. Атомный состав также может меняться в очень широких пределах. Однако экспериментальное изучение пространственного расположения узлов решетки показало, что число принципиально различных типов решеток ограничено. Двумерные решетки могут строиться с пространственным расположением узлов в виде следующих сеток: квадратной, прямоугольной, центрированно-прямоугольной, в форме параллелограмма или шестиугольника; последнюю можно альтернативным образом описать на основе ромбической ячейки с углами 60° (рис. 3.5)1.

Как было установлено французским кристаллографом Огюстом Браве (1811-1863), число трехмерных пространственных решеток ограничивается лишь 14 основными типами. На рис. 3 6 показано по одной элементарной ячейке для каждой из 14 таких решеток Браве. Любую элементарную ячейку можно рассматривать как кирпичик особой формы. Его можно уложить вместе с другими кирпичиками, относящимися к тому же типу (и имеющими те же размеры), таким образом, что образуется бесконечная пространственная постройка без каких-либо зазоров между отдельными кирпичиками. В любом конкретном минерале кирпичики (элементарные ячейки) можно считать идентичными, хотя на самом деле у них имеются незначительные различия, описанные в разд. 4.4.4.

Рис. 3.4 Одна из элементарных ячеек, показанных на рис 3.3 (хлу = 76°, a = 30 мм, b = 20 мм) Звезды Южного Креста характеризуются следующим образом

Координаты в мм	Координаты в единицах измерения а и 6
а	24, 18	0,8, 0,9
в	0,4	0,0; 0,2
7	4,5, 0,8	0,15, 0,4
д	О, 16	0,0, 0,8
£	28,5, 16,8	0,95, 0,84

Различные минеральные виды имеют элементарные ячейки разных типов, размеров и углов, если углы между ребрами не равны 90 или 120°.

Решетки Браве делятся на три группы (см. рис. 3.6):

1. Примитивные решетки P, в которых элементарная ячейка имеет узел решетки только в каждой своей вершине. Существует семь Р-решеток.

2. Объемноцентрированные решетки I (от немецкого слова mnenzentrierte), в которых узел решетки помимо того располагается в центре ячейки.

3. Гранецентрированные решетки с узлами в центрах всех граней (^-решетки) или в центрах одной пары граней (в разных случаях они называются по-разному: С — базоцентрирован-ные, А и В — бокоцентрированные).

Существование в кристаллах только 14 типов решеток подтверждается опытным путем. Рисунок 3.7 позволяет проверить наличие дополнительных решеток в тетрагональной сингонии. Из него следует, что возможные решетки либо уже входят в число 14 решеток Браве, либо не образуют пространственного расположения узлов, при-

Рис. 3.6 14 решеток Браве.

Рис. 3.7 Проверка возможности существования в тетрагональной системе дополнительных решеток.

сущего, согласно данному выше определению, истинной решетке.

Для описания кристаллической структуры требуется, чтобы ее решетка была определена в соответствии с имеющимися 14 типами, с дополнительным указанием размеров ребер и в необходимых случаях углов между ними.

Элементарная ячейка минерала, конечно, весьма невелика; если исходить из атомной шкалы размеров, то длины ребер ячейки составляют 0,3-0,7 HM. Посмотрим теперь, какое влияние эти крошечные ячейки оказывают на внешний облик кристаллов, который мы можем видеть и осязать.

3.1.3 Элементы внешней симметрии

Когда мы берем в руки хорошо образованный кристалл, то видим, что он обладает определенной симметрией. Для ее описания используются при веденные ниже элементы симметрии.

1. Поворотная ось. Если выбрана какая-либо ось, проходящая через объект, и в ходе его полного поворота вокруг этой оси одинаковое расположение элементов объекта наблюдается более чем один раз, то такой объект имеет поворотную ось симметрии. В кристаллах эта ось может быть двойной (второго порядка, или просто ось симметрии), тройной (третьего порядка), четверной (четвертого порядка) или шестерной (шестого порядка) осью симметрии в зависимости от того, сколько раз одна и та же картина повторяется за один полный поворот (рис. 3.8).

2. Плоскость симметрии (зеркальная плоскость). Если удается выбрать некоторую плоскость, проходящую через объект таким образом, что каждая его особенность по одну сторону плоскости имеет полностью эквивалентную особенность по ее другую сторону в зеркальном изображении, то она представляет собой плоскость симметрии (рис. 3.9).

3. Центр симметрии (см. также разд. 6.4.2). Когда каждый элемент на одной стороне объекта можно соединить проходящей через его центр воображаемой прямой на таком же расстоянии от него с аналогичным элементом на другой стороне, то этот объект имеет центр симметрии. Наличие центра симметрии можно проверить на модели кристалла следующим образом. Если положить модель на плоскость, то каждому пространственному (внешнему) углу, соприкасающемуся с плоскостью, должен соответствовать такой же угол, находящийся на противоположной (верхней) стороне в обратной позиции (рис. 3.10).

4. Ось инверсионных поворотов (инверсионная ось). Этот элемент несколько менее очевиден, чем предыдущие. Его сущность можно описать, если представить себе случай, когда в результате поворота с последующей инверсией через центр точка попадает в новое положение, но при повторении этого приема она возвращается в исходное положение (рис. 3.11). Инверсионные оси бывают первого порядка, двойные (инверсионная ось второго порядка), третьего, четвертого или шестого порядка и обозначаются 1,2,3,4,5,6 соответственно. Можно показать, что инверсионная ось проявляется как сочетание других, уже упомянутых элементов симметрии. Однако этот элемент является удобным дополнением к другим при различных построениях, показанных на рис. 3.37. Отметим, в частности, что 1 эквивалентно центру симметрии, а 2 — зеркальной плоскости m.

Для иллюстрации элементов симметрии на рис. 3.12 показаны те из них, которые присутствуют в основных семи типах элементарных ячеек примитивных решеток Браве. Читатель мог бы сам рассмотреть эти семь типов, используя деревянные или картонные модели соответствующей

Ось 2 Ось 4

Рис. 3.11 Инверсионные оси

формы. Ниже будет показано, что решетки, не относящиеся к примитивным (P), имеют внешнюю симметрию, соответствующую той или иной симметрии решеток P, т.е. имеется только семь различных групп симметрии.

Кристаллографическое использование

В кристаллической структуре геометрическая модель атома является геометрической структурой координации атомов, где определение координации атомов зависит от связей в модели. Например, в каменной соли, ионный состав каждого атома натрия содержит шесть ближайших соседних хлорид-ионов в октаэдрической геометрии и каждый хлорид аналогично — шесть соседних ионов натрия в октаэдрической геометрии. В металлах с объемноцентрированной структурой каждый атом имеет связь с восмью ближайшими другими атомами с кубической геометрией. В металлах с гранецентрированной кубической структурой каждый атом имеет двенадцать связей с соседними атомами с кубооктаэдрической геометрией.
Таблица координационной геометрии

Координационное число	Геометрия	Изображение	Примеры дискретных (конечных) комплексов	Примеры на кристаллах
2	линейная	Ag(CN)2− в KAg(CN)2	Ag в цианиде серебра,Au в AuI
3	плоский треугольник	Cu(CN)32− в Na2Cu(CN)3·3H2O	O в TiO2 (структура рутила)
4	тетраэдр	CoCl42−	Zn и S в сульфиде цинка, Si в диоксиде кремния
4	квадрат	AgF4−	CuO
5	тригональная бипирамидальная	SnCl5−
5	квадратная пирамидальная	InCl52− в (NEt4)2InCl5
6	октаэдр	Fe(H2O)62+	Na и Cl в хлориде натрия
6	тригональная призматическая	Mo(SCHCHS)3	As в NiAs, Mo в MoS2
7	пентагональная бипирамидальная	ZrF73− в (NH4)3ZrF7	Pa в PaCl5
7	гранецентрированная октаэдрическая	[HoIII(PhCOCHCOPh)3(H2O)]	La в La2O3
7	тригональная призматическая, квадратическая моногранецентрированная	TaF72− в K2TaF7
8	куб	Хлорид цезия, фторид кальция
8	квадратная антипризматическая	TaF83− в Na3TaF8	Хлорид тория(IV)
8	Mo(CN)84− в K4[Mo(CN)8].2H2O	Zr в K2ZrF6
8	гексагональная бипирамидальная	N в Li3N
8	октаэдр	Ni в арсениде никеля
8	Ca в CaFe2O4
8	тригональная призматическая, квадратная лицевая двуребристая	PuBr3
9	тригональная призматическая, квадратная лицевая триребристая	[ReH9]2− в нонагидроренате калия	SrCl2·6H2O , Th в RbTh3F13
9	англ. monocapped square antiprismatic	[Th(торополонат)4(H2O)]	La в LaTe2
10	англ. bicapped square antiprismatic	Th(C2O4)42−
11	Th в [ThIV(NO3)4(H2O)3] (NO3−)
12	икосаэдр	Th в Th(NO3)62−-ион в Mg[Th(NO3)6]·8H2O
12	кубооктаэдрон	ZrIV(η³−(BH4)4)
12
14	двуребристая антипризматичная гексагональная	U(BH4)4

Где нет дискретных комплексов означает, что соединения найдены как отдельные единицы сфер вокруг атомов в кристаллах

Элементарная ячейка, параметры решетки, виды элементарных ячеек, структурные типы.

Элементарные ячейки являются кирпичиками кристалла. Существует всего семь типов элементарных ячеек: кубическая, тетрагональная, гексагональная, тригональная, ромбическая, моноклинная и триклинная. Эти элементарные ячейки иногда называют примитивными, или сингониями. Каждая из сингоний представлена примитивной кристаллической ячейкой. Кроме того, существуют еще семь типов центрированных ячеек, которые содержат частицы на гранях и внутри ячейки. Всего существует 14 типов элементарных ячеек, которые называются решетками Браве, по имени французского ученого, который показал, что любую ячейку можно преобразовать в одну из 14. Чтобы выбрать ячейку, наиболее полно отражающую все особенности данной решетки, нужно придерживаться следующих правил:

симметрия ячейки должна соответствовать симметрии решетки в целом;

число прямых углов в ячейке должно быть максимальным;

объем ячейки должен быть минимальным.

Объемо Кристалли́ческая структу́ра — такая совокупность атомов, в которой с каждой точкой кристаллической решётки связана определённая группа атомов, называемая мотивной единицей, причём все такие группы одинаковые по составу, строению и ориентации относительно решётки. Можно считать, что структура возникает в результате синтеза решётки и мотивной единицы, в результате размножения мотивной единицы группой трансляции.

В простейшем случае мотивная единица состоит из одного атома, например в кристаллах меди или железа. Возникающая на основе такой мотивной единицы структура геометрически весьма сходна с решёткой, но все же отличается тем, что составлена атомами, а не точками. Часто это обстоятельство не учитывают, и термины «кристаллическая решётка» и «кристаллическая структура» для таких кристаллов употребляются как синонимы, что нестрого. В тех случаях, когда мотивная единица более сложна по составу — состоит из двух или большего числа атомов, геометрического сходства решётки и структуры нет, и смешение этих понятий приводит к ошибкам. Так, например, структура магния или алмаза не совпадает геометрически с решёткой: в этих структурах мотивные единицы состоят из двух атомов.

Основными параметрами, характеризующими кристаллическую структуру, некоторые из которых взаимосвязаны, являются следующие:

• тип кристаллической решётки (сингония, решётка Браве);

• число формульных единиц, приходящихся на элементарную ячейку;

• пространственная группа;

• параметры элементарной ячейки (линейные размеры и углы);

координаты атомов в ячейке;

Структура кристалла − это конкретное расположение частиц в пространстве. Описывая структуру, необходимо указать вид и размер частиц, а также расстояния между ними. Если вещества кристаллизуются в сходных друг с другом решетках, то говорят, что они относятся к одному структурному типу

. У кристаллов, принадлежащих к одному структурному типу, элементарные ячейки одинаковы с точностью до подобия. Опишем некоторые наиболее часто встречающиеся структурные типы [27, 83].

Опытные данные показывают, что почти 80 % металлов кристаллизуются в объемно- и гранецентрированных кубических, а также в гексагональных плотноупакованных решетках.

Билет 5

Атомная координация

Рассматривая расположение атомов относительно друг друга, их координационные числа (или количество ближайших соседей), межатомные расстояния, типы связи и т. Д., Можно сформировать общее представление о структурах и альтернативных способах их визуализации.

Тесная упаковка

Решетка ГПУ (слева) и решетка ГЦК (справа)

Используемые принципы можно понять, рассмотрев наиболее эффективный способ упаковки сфер одинакового размера и укладки плотно упакованных атомных плоскостей в трех измерениях. Например, если плоскость A лежит ниже плоскости B, есть два возможных способа размещения дополнительного атома поверх слоя B. Если дополнительный слой был помещен непосредственно над плоскостью A, это привело бы к следующей серии:

…
АБАБАБАБ
…

Такое расположение атомов в кристаллической структуре известно как гексагональная плотная упаковка (ГПУ)

Если, однако, все три плоскости расположены в шахматном порядке относительно друг друга и последовательность повторяется только после того, как четвертый слой будет расположен непосредственно над плоскостью A, тогда возникает следующая последовательность:

…
ABCABCABC
…

Этот тип структурного устройства известен как кубическая плотная упаковка (ccp)

Элементарной ячейкой ccp-расположения атомов является гранецентрированная кубическая (ГЦК) элементарная ячейка. Это не сразу очевидно, поскольку плотно упакованные слои параллельны плоскостям {111} элементарной ГЦК-ячейки. Есть четыре различных ориентации плотноупакованных слоев.

Эффективность упаковки

может быть разработана путем расчета общего объема сфер и деления на объеме ячейки следующим образом :
4×43πр3162р3знак равноπ32знак равно0,7405 …{\ displaystyle {\ frac {4 \ times {\ frac {4} {3}} \ pi r ^ {3}} {16 {\ sqrt {2}} r ^ {3}}} = {\ frac {\ pi} {3 {\ sqrt {2}}}} = 0,7405 …}
Эффективность упаковки 74% – это максимальная плотность, возможная для элементарных ячеек, построенных из сфер только одного размера. Большинство кристаллических форм металлических элементов – это ГПУ, ГЦК или ОЦК (объемно-центрированная кубическая). Координационное число атомов в ГПУ и ГЦК структуры 12 и ее атомный фактор упаковки (ПФ) это число упоминалось выше, 0,74. Это можно сравнить с APF ОЦК-структуры, равным 0,68.

Что такое кристаллическая решетка

Как известно, все вещества состоят из частиц — атомов, которые могут располагаться хаотично или в определенном порядке. У аморфных веществ частицы расположены беспорядочно, а у кристаллических они образуют определенную структуру. Эта структура называется кристаллической решеткой. Она определяет такие характеристики вещества, как твердость, хрупкость, температура кипения и/или плавления, пластичность, растворимость, электропроводность и т. д.

Кристаллическая решетка — это внутренняя структура кристалла, порядок взаимного расположения атомов, ионов или молекул. Точки, в которых находятся эти частицы, называются узлами решетки.

Частицы удерживаются на своих местах благодаря химическим связям между ними. В зависимости от того, какой вид связи удерживает атомы или ионы данного вещества, в химии выделяют основные типы кристаллических решеток:

атомная (ковалентные связи),
молекулярная (ковалентные связи и притяжение между молекулами),
металлическая (металлические связи),
ионная (ионные связи).

Важно!

Не путайте эти два понятия — кристаллическая решетка и химическая связь. Тип решетки говорит о том, как расположены атомы/ионы в молекуле вещества, а тип связи — по какому принципу они между собой взаимодействуют.

Наличие порядка в расположении частиц

В аморфном веществе, в отличие от кристаллического, отсутствует какой-либо порядок в расположении частиц. Если же в кристаллическом веществе мысленно соединить прямой два близкоросположенных друг к другу атома, то можно обнаружить, что на этой линии на строго определенных промежутках будут лежать одни и те же частицы:

Таким образом, в случае кристаллических веществах можно говорить о таком понятии, как кристаллическая решетка.

Кристаллической решеткой называют пространственный каркас, соединяющий точки пространства, в которых находятся частицы, образующие кристалл.

Точки пространства, в которых находятся образующие кристалл частицы, называют узлами кристаллической решетки.

В зависимости от того, какие частицы находятся в узлах кристаллической решетки, различают: молекулярную, атомную, ионную и металлическую кристаллические решетки.

В узлах молекулярной кристаллической решетки Кристаллическая решетка льда Кристаллическая решетка льда как пример молекулярной решетки

находятся молекулы, внутри которых атомы связаны прочными ковалентными связями, однако сами молекулы удерживаются друг возле друга слабыми межмолекулярными силами. Вследствие таких слабых межмолекулярных взаимодействий кристаллы с молекулярной решеткой являются непрочными. Такие вещества от веществ с иными типами строения отличаются существенно более низкими температурами плавления и кипения, не проводят электрический ток, могут как растворяться, так и не растворяться в различных растворителях.

Растворы таких соединений могут как проводить, так и не проводить электрический ток в зависимости от класса соединения. К соединениям с молекулярной кристаллической решеткой относятся многие простые вещества — неметаллы (отвержденные H2, O2, Cl2, ромбическая сера S8, белый фосфор P4), а также многие сложные вещества – водородные соединения неметаллов, кислоты, оксиды неметаллов, большинство органических веществ. Следует отметить, что, если вещество находится в газообразном или жидком состоянии, говорить о молекулярной кристаллической решетке неуместно: корректнее использовать термин — молекулярный тип строения.

кристаллическая решетка алмаза Кристаллическая решетка алмаза как пример атомной решетки В узлах атомной кристаллической решетки

находятся атомы. При этом все узлы такой кристаллической решетки «сшиты» между собой посредством прочных ковалентных связей в единый кристалл. Фактически, такой кристалл является одной гигантской молекулой. Вследствие особенностей строения все вещества с атомной кристаллической решеткой являются твердыми, обладают высокими температурами плавления, химически мало активны, не растворимы ни в воде, ни в органических растворителях, а их расплавы не проводят электрический ток. Следует запомнить, что к веществам с атомным типом строения из простых веществ относятся бор B, углерод C (алмаз и графит), кремний Si, из сложных веществ — диоксид кремния SiO2 (кварц), карбид кремния SiC, нитрид бора BN.

У веществ с ионной кристаллической решеткой в узлах решетки находятся ионы, связанные друг с другом посредством ионных связей.

Поскольку ионные связи достаточно прочны, вещества с ионной решеткой обладают сравнительно высокой твердостью и тугоплавкостью. Чаще всего они растворимы в воде, а их растворы, как и расплавы проводят электрический ток. К веществам с ионным типом кристаллической решетки относятся соли металлов и аммония (NH4+), основания, оксиды металлов. Верным признаком ионного строения вещества является наличие в его составе одновременно атомов типичного металла и неметалла.

Кристаллическая решетка хлорида натрия

Кристаллическая решетка хлорида натрия как пример ионной решетки Однако следует отметить, что в веществах с ионным типом строения нередко можно обнаружить, помимо ионных, также ковалентные полярные связи. Это наблюдается в случае сложных ионов, т.е. состоящих из двух или более химических элементов (SO42-, NH4+, PO43- и т.д.). Внутри таких сложных ионов атомы связаны друг с другом ковалентными связями.

Металлическая кристаллическая решетка

наблюдается в кристаллах свободных металлов, например, натрия Na, железа Fe, магния Mg и т.д. В случае металлической кристаллической решетки, в ее узлах находятся катионы и атомы металлов, между которыми движутся электроны. При этом движущиеся электроны периодически присоединяются к катионам, таким образом нейтрализуя их заряд, а отдельные нейтральные атомы металлов взамен «отпускают» часть своих электронов, превращаясь, в свою очередь, в катионы. Фактически, «свободные» электроны принадлежат не отдельным атомам, а всему кристаллу.

Кристаллическая решетка

Все твердые тела по внутренней структуре можно классифицировать на две формы: аморфные и кристаллические. Отличительной особенностью последних является специфическая организованная структура частиц.

Кристаллическая решетка – это упрощенная трехмерная модель твердых кристаллов, которая используется для анализа их свойств в физике, химии, биологии, минералогии и других науках. Внешне она похожа на сетку. В ее узлах находятся атомы вещества. Данный массив точек имеет определенный, регулярно повторяющийся порядок, специфичный для каждого вида вещества.

Прогнозирование структуры

Сложность предсказания стабильных кристаллических структур на основе знания только химического состава долгое время была камнем преткновения на пути к полностью вычислительному дизайну материалов. Теперь, благодаря более мощным алгоритмам и высокопроизводительным вычислениям, структуры средней сложности могут быть предсказаны с использованием таких подходов, как эволюционные алгоритмы , случайная выборка или метадинамика.

Кристаллические структуры простых ионных твердых веществ (например, NaCl или поваренная соль) уже давно рационализированы с точки зрения правил Полинга , впервые изложенных в 1929 году Линусом Полингом , которого многие с тех пор называют «отцом химической связи». Полинг также рассмотрел природу межатомных сил в металлах и пришел к выводу, что около половины из пяти d-орбиталей в переходных металлах участвуют в связывании, а оставшиеся несвязывающие d-орбитали ответственны за магнитные свойства. Таким образом, он смог соотнести количество d-орбиталей в образовании связи с длиной связи, а также со многими физическими свойствами вещества. Впоследствии он ввел металлическую орбиталь, дополнительную орбиталь, необходимую для разрешения неограниченного резонанса валентных связей между различными электронными структурами.

В теории резонансных валентных связей факторы, определяющие выбор одной из альтернативных кристаллических структур металла или интерметаллического соединения, вращаются вокруг энергии резонанса связей между межатомными положениями. Ясно, что некоторые режимы резонанса будут давать больший вклад (будут более механически устойчивыми, чем другие), и что, в частности, простое соотношение количества связей к количеству позиций будет исключительным. Результирующий принцип заключается в том, что особая стабильность связана с простейшими соотношениями или «числами облигаций»: 1 ⁄ 2 , 1 ⁄ 3 , 2 ⁄ 3 , 1 ⁄ 4 , 3 ⁄ 4 и т. Д. Выбор структуры и значения осевое отношение (которое определяет относительные длины связей), таким образом , является результатом усилий атома , чтобы использовать его валентность в формировании стабильных связей с простыми дробными числами облигаций.

Постулируя прямую корреляцию между концентрацией электронов и кристаллической структурой в сплавах с бета-фазой, Хьюм-Розери проанализировал тенденции изменения точек плавления, сжимаемости и длин связей в зависимости от номера группы в периодической таблице, чтобы установить систему валентностей переходные элементы в металлическом состоянии. Таким образом, эта обработка подчеркнула увеличение прочности сцепления в зависимости от номера группы. Действие направленных сил было подчеркнуто в одной статье о связи между связующими гибридами и металлическими структурами. Результирующая корреляция между электронными и кристаллическими структурами резюмируется одним параметром, весом d-электронов на гибридизованную металлическую орбиталь. «D-вес» составляет 0,5, 0,7 и 0,9 для структур ГЦК, ГПУ и ОЦК соответственно. Таким образом, становится очевидной связь между d-электронами и кристаллической структурой.

При прогнозировании / моделировании кристаллической структуры обычно применяется периодичность, поскольку система представляется неограниченно большой во всех направлениях. Начиная с триклинной структуры без дополнительных предполагаемых свойств симметрии, систему можно заставить показать некоторые дополнительные свойства симметрии, применив Второй закон Ньютона к частицам в элементарной ячейке и недавно разработанное динамическое уравнение для векторов периодов системы (параметры решетки, включая углы ), даже если система подвергается внешним нагрузкам.

Виды

В науке выделяют 14 видов элементарных ячеек решеток, обладающих уникальной геометрией. Впервые их описал французский физик Огюст Бравэ в 1848 г. Этого ученого считают основателем кристаллографии.

Данные типы элементарных структур кристаллической решетки группируют в 7 категорий, называемых сингониями, в зависимости от соотношения длин сторон и равенства углов:

кубическая;
тетрагональная;
орторомбическая;
ромбоэдрическая;
шестиугольная;
триклинная.

Наиболее простой и распространенной в природе из них является первая категория, которая в свою очередь делится на 3 типа решеток:

Простая кубическая. Все частицы (а ими могут быть атомы, электрически заряженные частицы или молекулы) находятся в вершинах куба. Эти частицы идентичны. Каждой ячейке принадлежит 1 атом (8 вершин × 1/8 атома = 1).
Объемноцентрированная кубическая. Отличается от предыдущей модели тем, что в центре куба находится еще одна частица. К каждой ячейке относится по 2 атома вещества.
Гранецентрированная кубическая. Частицы содержатся в вершинах элементарной ячейки, а также в центре всех граней. Каждая из ячеек насчитывает по 4 атома.

Обратные решетки различных кристаллов

Обратные решетки для кубической кристаллической системы следующие.

Простая кубическая решетка

Простая кубическая решетка Браве с кубической примитивной ячейкой стороны имеет в качестве обратной стороны простую кубическую решетку с кубической примитивной ячейкой стороны ( в определении кристаллографа). Поэтому кубическая решетка называется самодуальной, имеющей ту же симметрию в обратном пространстве, что и в реальном пространстве. а{\ displaystyle a}2πа{\ displaystyle \ textstyle {\ frac {2 \ pi} {a}}}1а{\ displaystyle \ textstyle {\ frac {1} {a}}}

Гранецентрированная кубическая (ГЦК) решетка

Обратной решеткой для ГЦК-решетки является объемно-центрированная кубическая (ОЦК) решетка со стороной куба . 4πа{\ displaystyle \ textstyle {\ frac {4 \ pi} {a}}}

Рассмотрим составную элементарную ячейку FCC. Найдите примитивную элементарную ячейку FCC; т.е. элементарная ячейка с одной точкой решетки. Теперь возьмем за начало координат одну из вершин примитивной элементарной ячейки. Приведите базисные векторы реальной решетки. Затем по известным формулам можно вычислить базисные векторы обратной решетки. Эти векторы обратной решетки FCC представляют собой базисные векторы реальной решетки BCC

Обратите внимание, что базисные векторы реальной решетки ОЦК и обратной решетки ГЦК похожи друг на друга по направлению, но не по величине.

Объемно-центрированная кубическая (ОЦК) решетка

Обратной решеткой ОЦК- решетки является ГЦК- решетка со стороной куба . 4πа{\ displaystyle \ textstyle {\ frac {4 \ pi} {a}}}

Можно легко доказать, что только решетки Браве с углом между ними 90 градусов (кубический, тетрагональный, ромбический) имеют векторы , параллельные своим векторам в реальном пространстве. (а1,а2,а3){\ displaystyle \ left (\ mathbf {a} _ {1}, \ mathbf {a} _ {2}, \ mathbf {a} _ {3} \ right)}(б1,б2,б3){\ displaystyle \ left (\ mathbf {b} _ {1}, \ mathbf {b} _ {2}, \ mathbf {b} _ {3} \ right)}

Простая шестиугольная решетка

Обратный к простой гексагональной решетке Бравы с решеткой константой с и другим простым гексагональной решеткой с постоянными решетками и повернута на 30 ° вокруг оси с относительно прямой решетки. Поэтому простая гексагональная решетка называется самодуальной, имеющей ту же симметрию в обратном пространстве, что и в реальном пространстве. векторы a 1 = (a (3) 1/2 / 2) i + (a / 2) j; a 2 = – (a (3) 1/2 / 2) i + (a / 2) j ve a 3 = ak 2πc{\ displaystyle \ textstyle {\ frac {2 \ pi} {c}}}4πа3{\ displaystyle \ textstyle {\ frac {4 \ pi} {a {\ sqrt {3}}}}}

Типы кристаллических решеток

Home / Определения Глоссария / Типы кристаллических решеток

Кристалл с определенной химической формулой имеет присущую ему кристаллическую структуру. Кристаллические структуры — это структуры, представляющие периодическую решетку, в узлах которой расположены атомы. Трехмерная кристаллическая структура представляет решетку, построенную на трех координатных осях x, y, z, расположенных в общем случае под углами a, b, g . Периоды трансляции атомов по осям (параметры решетки) равны, соответственно, a, b, c. Элементарная ячейка кристалла — это параллелепипед, построенный на векторах трансляции a, b, c. Такая ячейка называется примитивной. В результате трансляции элементарной ячейки в пространстве получается пространственная простая решетка — так называемая решетка Браве. Существует четырнадцать типов решеток Браве. Эти решетки отличаются друг от друга видом элементарных ячеек.

Решетки Браве подразделяются на семь систем, называемых кристаллографическими сингониями, в соответствии с семью различными типами элементарных ячеек: триклинной, моноклинной, ромбической, тетрагональной, тригональной, кубической и гексагональной. Эти элементарные ячейки могут быть как примитивными, так и сложными. На рисунке изображены сложные элементарные ячейки.

а)объемноцентрированная б)гранецентрированная в) базоцентрированная г) гексагональная

Объемноцентрированная (ОЦ) ячейка (рис. а) — содержит дополнительно один атом на пересечении пространственных диагоналей куба (или, в общем случае, параллелепипеда). В ОЦ кубической структуре (ОЦК) кристаллизуются такие металлы, как 23V, 24Cr, 26Fe, 41Nb, 73Ta, 74W (индекс слева внизу обозначает номер элемента в периодической системе элементов Д. И. Менделеева). Гранецентрированная (ГЦ) ячейка (рис. б) — содержит дополнительно по одному атому в плоскости каждой грани. В ГЦ кубической структуре (ГЦК) кристаллизуются металлы 13Al, 28Ni, 29Cu, 47Ag, 78Pt, 79Au и др. Базоцентрированная (БЦ) ячейка (рис. в) — содержит дополнительно по одному атому в центрах противоположных граней. Гексагональная ячейка (рис. г) состоит из трех примитивных ячеек, и, как и БЦ ячейка, содержит по одному атому в центре противоположных граней. В гексагональной структуре кристаллизуются многие металлы — 22Ti, 27Co, 30Zn, 39Y, 40Zr, 64Gd, 71Lu. Различные кристаллографические систем отличаются друг от друга формой элементарной ячейки: соотношениями между длинами ребер a, b и c и углами α, β и γ между гранями. В триклинной системе (где нет осей и плоскостей симметрии) такая ячейка представляет собой параллелепипед, все ребра и углы которого не равны между собой. В моноклинной — это наклонный параллелепипед; в ромбической (или орторомбической) — прямоугольный параллелепипед с неравными ребрами, в тетрагональной — прямоугольный параллелепипед, в основании которого лежит квадрат; в тригональной (ромбоэдрической) — прямоугольный ромбоэдр, стороны которого равны, а углы одинаковы, но отличны от 90о и меньше, чем 120о; в гексагональной — прямую призму, основанием которой является ромб с углами 120о и 60о, а три ячейки составляют шестигранную призму; в кубической системе элементарная ячейка представляет собой куб.

В настоящее время выделено уже более тысячи структурных типов, однако они охватывают лишь несколько процентов известных кристаллических структур. В международной классификации по группам структур принята следующая классификация: А — элементы; В — соединения типа АВ (например, NaCl, CsI); С — соединения типа AB2 (CaF2, TiO2); D — соединения типа AnBm (Al2O3); E — соединения, образованные больше, чем двумя сортами атомов без радикалов или комплексных ионов (например, CuFeS); F -структуры соединений с двух- или трехатомными ионами (KCNS, NaHF2); G — соединения с четырехатомными ионами (CaCO3, NaClO3); H — соединения с пятиатомными ионами (CaSО4.2H2O, CaWO4); L — сплавы; S -силикаты. Разновидности типов внутри группы различаются номерами.

Понятие структурный тип — один из критериев сходства или различия строения кристаллов. Обычно структурный тип относят к названию одного из веществ, кристаллизующихся в нём. Структуры кристаллов, принадлежащих к одному структурному типу, одинаковы до подобия. Структурный тип в кристаллографии определяет относительное расположение частиц (атомов или атомных групп) в кристалле, без указаний абсолютных расстояний между ними. Чтобы описать конкретную структуру, надо указать структурный тип и параметры структуры. К важнейшим и распространенным структурным типам относятся: структура меди (тип А), структура вольфрама (тип А 2), структура магния (тип А 3), структура алмаза (тип А 4), структура графита (тип А 9), структура каменной соли (тип В 1), структура перовскита (тип Е 2), структура шпинели (тип Н 11).

Тип А (Структура меди) В структурном типе меди кристаллизуются очень многие металлы: золото, серебро, никель, алюминий, кальций, торий, свинец и др. Все эти металлы сравнительно мягкие, пластичные, легко обрабатываются. Многие из них образуют непрерывные ряды твердых растворов , например, Ag-Au, Cu-Au. Структурой типа меди обладают также интерметаллические соединения AuSb, Au2Bi, Au2Pb, Cu2Mg, Bi2K, ZrH, TiH и др. Элементарная ячейка меди — кубическая, гранецентрированная. Атомы располагаются в вершинах и центрах граней F -ячейки. На элементарную ячейку приходится 4 атома. Каждый атом окружен 12 ближайшими атомами, координационное число (к.ч.) =12. Координационный многогранник — кубооктаэдр. В структуре имеется одна правильная система точек с кратностью 4. Плотнейшие слои 1 перпендикулярны направлениям . Плотнейшая упаковка кубическая трехслойная ….АВСАВС….Пространственная группа Fm3m.

Тип А 2 (Структура вольфрама) К структурному типу вольфрама (тип ОЦК-металлов) относятся тугоплавкие металлы: хром, ванадий, молибден, ниобий, тантал, -кобальт, -железо, титан, цирконий, гафний, щелочные элементы — литий, натрий, калий, рубидий, цезий, щелочноземельные — кальций, стронций, барий, актиниды — уран, нептуний, плутоний. Из интерметаллических соединений в ОЦК-структуре кристаллизуются AgZn, Cu3Al, CoAl, Cu5Sn, LiAg, LiAl, TaH и др. В объемно-центрированной кубической ячейке вольфрама атомы располагаются по вершинам и в центре ячейки, т.е. на одну ячейку приходится два атома. ОЦК-структура не является плотнейшей упаковкой атомов. Коэффициент компактности равен 0,68. Пространственная группа вольфрама Im3m. Тип А3 (Структура магния) В структурном типе магния кристаллизуются гексагональные металлы: кадмий, бериллий, таллий, титан, никель, хром и др. Эта структура также характерна для интерметаллических соединений AgCd, AgCd3, AuCd, AuCd3, CuCd3, AgZn3, AuZn3, NiMo, TiH, W2С и др. Элементарная ячейка магния — элементарная примитивная. Центры атомов располагаются по вершинам правильных шестиугольников: в трех вершинах — через одну, — атомы верхнего слоя, в трех других вершинах — атомы нижнего слоя. Элементарная ячейка построена на трех трансляциях, две из которых лежат в плотно упакованном слое атомов и составляют между собой угол = 120о, третья перпендикулярна этому слою. Элементарную ячейку можно разделить плоскостью на две тригональные призмы. В центре одной из призм расположен атом, другая свободна, заселенные и пустые призмы чередуются между собой. На элементарную ячейку приходится два атома магния. Каждый атом магния окружен двенадцатью ближайшими атомами: шестью — в том же слое, тремя в соседнем слое сверху и тремя в соседнем слое снизу, к.ч.=12. Плотные слои — плоскости базиса (0001), упаковка гексагональная, двухслойная ….АВАВАВАВ…. Кристаллы металлов с плотно упакованной гексагональной структурой легче всего деформируются по плоскостям (0001) и направлениям , соответствующим наиболее плотной упаковке атомов. Координационный многогранник — гексагональный кубооктаэдр. Пространственная группа магния Р63/mmc.

Общее понятие о металлах

«Химия. 9 класс» — это учебник, по которому проходят обучение школьники. Именно в нем подробно изучаются металлы. Рассмотрению их физических и химических свойств отведена большая глава, ведь разнообразие их чрезвычайно велико.

Именно с этого возраста рекомендуют давать детям представление о данных атомах и их свойствах, ведь подростки уже вполне могут оценить значение подобных знаний. Они прекрасно видят, что окружающее их разнообразие предметов, машин и прочих вещей имеет в своей основе как раз металлическую природу.

Что же такое металл? С точки зрения химии, к данным атомам принято относить те, что имеют:

малое число электронов на внешнем уровне;
проявляют сильные восстановительные свойства;
имеют большой атомный радиус;
как простые вещества обладают рядом специфических физических свойств.

Основу знаний об этих веществах можно получить, если рассмотреть атомно-кристаллическое строение металлов. Именно оно объясняет все особенности и свойства данных соединений.

В периодической системе для металлов отводится большая часть всей таблицы, ведь они образуют все побочные подгруппы и главные с первой по третью группу. Поэтому их численное превосходство очевидно. Самыми распространенными являются:

Все металлы имеют ряд свойств, которые позволяют объединять их в одну большую группу веществ. В свою очередь, эти свойства объясняет именно кристаллическое строение металлов.

Объемно-центрированная решетка

Строение кристаллической решетки металлов данного типа представляет собой следующую структуру. Это куб, в узлах которого находится восемь атомов. Еще один располагается в центре свободного внутреннего пространства ячейки, что и объясняет название “объемно-центрированная”.

Это один из вариантов наиболее простого строения элементарной ячейки, а значит, и всей решетки в целом. Такой тип имеют следующие металлы:

молибден;
ванадий;
хром;
марганец;
альфа-железо;
бетта-железо и другие.

Основные свойства таких представителей – высокая степень ковкости и пластичности, твердость и прочность.

Что такое элементарная ячейка?

Элементарная ячейка кристаллической решетки – это наименьшая часть твердого тела, которая позволяет охарактеризовать его свойства. Она служит основой решетки и дублируется в ней бесчисленное количество раз.

Данная модель используется для упрощения визуального описания внутреннего строения кристаллов. При этом применяется система из 3 кристаллографических координатных осей, которые отличаются от обычных ортогональных тем, что они являются конечными отрезками определенного размера. Углы между осями могут быть равны 90° или быть непрямыми.

Если плотно заполнить элементарными ячейками определенный объем, то можно получить идеальный монокристалл. На практике более распространены поликристаллы, состоящие из нескольких ограниченных в пространстве регулярных структур.

Пустоты в элементарной ячейке

Визуализация кубической элементарной ячейки алмаза: 1. Компоненты элементарной ячейки, 2. Одна элементарная ячейка, 3. Решетка из 3 x 3 x 3 элементарных ячеек.

Простая кубическая элементарная ячейка имеет одну кубическую пустоту в центре.

Объемно-центрированная кубическая элементарная ячейка имеет шесть октаэдрических пустот, расположенных в центре каждой грани элементарной ячейки, и двенадцать дополнительных, расположенных в середине каждого края той же ячейки, в общей сложности шесть октаэдрических пустот. Кроме того, есть 24 тетраэдрических пустоты, расположенных на квадратном расстоянии вокруг каждой октаэдрической пустоты, в общей сложности двенадцать чистых тетраэдрических пустот. Эти тетраэдрические пустоты не являются локальными максимумами и технически не являются пустотами, но иногда они появляются в многоатомных элементарных ячейках.

Гранецентрированная кубическая элементарная ячейка имеет восемь тетраэдрических пустот, расположенных на полпути между каждым углом и центром элементарной ячейки, всего восемь чистых тетраэдрических пустот. Вдобавок есть двенадцать октаэдрических пустот, расположенных в средних точках краев элементарной ячейки, а также одно октаэдрическое отверстие в самом центре ячейки, всего четыре чистых октаэдрических пустот.

Одной из важных характеристик кристаллической структуры является фактор упаковки атомов . Это рассчитывается исходя из предположения, что все атомы являются идентичными сферами, с радиусом, достаточно большим, чтобы каждая сфера упиралась в следующую. Фактор атомной упаковки – это доля пространства, заполненного этими сферами.

Предполагая , один атом за решетку точки, в примитивной кубической решетке с длиной стороны кубы а

, радиус шара будет 2 и атомный фактор упаковки оказывается около 0,524 (что является довольно низким). Точно так же в
ОЦК
решетке фактор упаковки атомов составляет 0,680, а в
ГЦК
– 0,740. Значение
ГЦК
является наивысшим теоретически возможным значением для любой решетки, хотя есть и другие решетки, которые также достигают того же значения, например гексагональная плотноупакованная (
ГПУ
) и одна версия тетраэдрической
ОЦК
.

Как правило, поскольку атомы в твердом теле притягиваются друг к другу, более плотно упакованные атомы имеют тенденцию быть более распространенным. (Хотя могут иметь место неплотно упакованные структуры, например, если орбитальная гибридизация требует определенных валентных углов .) Соответственно, примитивная кубическая структура с особенно низким коэффициентом упаковки атомов встречается редко в природе, но встречается в полонии . ОЦК

и
ГЦК
, с их более высокой плотностью, оба довольно широко распространены в природе. Примеры
ОЦК
включают железо , хром , вольфрам и ниобий . Примеры
ГЦК
включают алюминий , медь , золото и серебро .

Кристаллическая решётка. Элементарная ячейка

Структура кристалла– это конкретное расположение частиц в пространстве (физическая реальность). Чтобы представить структуру кристалла, нужно знать относительные размеры частиц, расстояния между ними, силы связи между частицами, их взаимное расположение, повторяющее расположение частиц в пространстве (пространственную решётку), и законы симметрических преобразований.

Симметрия– основная особенность, характерная для структуры кристаллов. Теорию строения структуры кристаллов развил английский учёный Бравэ, основываясь на многих экспериментальных результатах других исследователей. Положив в основу своей теории анизотропию и симметрию кристаллов, он пришёл к понятию о пространственной решётке.

Пространственная решётка– это способ представления периодичности повторения в пространстве отдельных материальных частиц или групп частиц. Кристаллическая решётка– пространственная сетка, в узлах которой располагаются частицы (атомы, ионы, молекулы), образующие кристалл. Основу кристалла, её остов, каркас можно представить как бесконечную решётку, состоящую из множества одинаковых смежных параллелепипедов — ячеек Бравэ (рис. 1.11). Например, кристаллическая решётка поваренной соли NaCl представляет собой две кубические решётки с атомами хлора и атомами натрия в узлах, «вставленные» одна в другую (рис. 1.8). Какова бы ни была кристаллическая решётка, описывающая структуру кристалла, в её основе всегда лежат ячейки Бравэ.

Рис. 1.11.Пространственные решётки некоторых веществ

Рассмотрим простейший случай, когда одинаковые частицы расположены в кристалле параллельными бесконечными рядами. На 1 мм в кристалле находится порядка 107 частиц (рис. 1.12). Трансляция(период идентичности) –симметричное преобразование, при котором точка (частица) повторяется в пространстве. Её величина – кратчайшее из возможных расстояний между одинаковыми точками в ряду.

Рис. 1.12.Линейная цепочка атомов

Если сдвинуть точки бесконечного ряда на один период идентичности вдоль направления трансляции, то ряд совместится сам с собой, его вид не нарушится. Выбор основных трансляций в структуре кристалла очень важен, потому что ими определяются кристаллографические системы координат. В общем случае это косоугольные координаты с разными масштабными отрезками по осям (рис. 1.13).

Узлы ряда– одинаковые точки, связанные между собой величиной трансляции ав бесконечном ряду. При перенесении точек по трём направлениям на величину трансляций а, b, c можнополучить трёхмерную сетку.

Ячейки сетки– параллелограммы, вершины которых являются узлами.

Элементарная ячейка– параллелепипед с характерным для данной решётки расположением частиц, с помощью которого весь кристалл может быть построен путём его многократного повторения в трёх направлениях. Она строится на трёх элементарных трансляциях а, b, с. Элементарную ячейку принято выбирать так, чтобы она удовлетворяла следующим условиям: наилучшим образом отражала симметрию сетки, имела бы прямые углы и, если возможно, обладала бы наименьшим объёмом.

Примитивнойназывается элементарная ячейка, внутри которой нет узлов, частицы содержатся только в вершинах (рис. 1.13). Узлы решётки– вершины ячеек, в которых располагаются одинаковые атомы или группы атомов. Они эквивалентны друг другу.

Период (постоянная) кристаллической ячейки– расстояние между однородными атомами. Параметры элементарной ячейки: три ребра ячейки a, b, c; три угла между ними α, β, γ. Например, для представленной на рис. 1.13 примитивной ячейки, соотношения между параметрами следующие:

Рис. 1.13.Примитивная элементарная ячейка

Элементарные ячейки, составляющие кристаллическую решётку кристалла, имеют одинаковые форму и объём. Кристалл можно построить с помощью разных примитивных ячеек. В некоторых случаях удобно характеризовать пространственную сетку не примитивной, а сложной элементарной ячейкой, у которой узлы есть не только в вершинах, но и внутри ячейки. Элементарная ячейка может содержать несколько примитивных ячеек.

Элементарные ячейкиразличаются по элементам симметрии и степени заполнения атомами (рис. 1.14).

Рис. 1.14.Разные примитивные ячейки в плоской сетке

К элементам симметрииотносятся: трансляции, плоскости симметрии, зеркальные плоскости, оси симметрии разных порядков, инверсионные оси симметрии (рис. 1.15).

Рис. 1.15. Элементы симметрии в кубическом кристалле

Кристаллические ячейки делятся по элементам симметрии на 7 сингоний:триклинная, моноклинная, ромбическая, ромбоэдрическая, гексагональная, тетрагональная, кубическая. Сингония в дословном переводе – сходноугольность. В сингонию объединяют кристаллы, у которых одинакова симметрия элементарных ячеек и одинаковая система координат.На рис. 1.16 показана тетрагональная ячейка.

Рис. 1.16. Кристаллическая ячейка тетрагональной сингонии

В каждой сингонии элементарные ячейки делятся по степени заполнения их атомами. Так на одну ячейку простой кубической ячейки имеет приходится 1 атом: n = (1/8)8 = 1; объёмноцентрированной кубической ячейки (ОЦК) – 2 атома: n = (1/8)8 + 1 = 2; гранецентрированной кубической ячейки (ГЦК) – 4 атома: n =(1/8)8 + (1/2)6 = 4 Рис. 1.17); гексагональной с плотной упаковкой (ГПУ) – 2 атома.

Рис. 1.17. Кристаллические ячейки

Кристаллическую решетку общего типа называют решеткой с базисом(БЦК). Решетка с базисом представляется в виде двух вставленных одна в другую подрешеток Бравэ, каждая из которых определяется трансляционными векторами. Базисный вектор устанавливает смещение решеток друг относительно друга. Количество базисных векторов может быть сколь угодно большим.

Рис. 1.18.Решётки Браве

Все известные в природе кристаллические тела кристаллизуются в 14 решётках Браве(рис. 1.18). Далее они делятся на 32 класса симметрии и 230 пространственных групп.

Некоторым телам свойственна не одна, а две или более кристаллических структур, устойчивых при различных температурах и давлениях. Такое явление называется полиморфизмом.Полиморфные формы (модификациивещества) имеют, например, углерод и олово. Углеродможет существовать в виде алмаза и графита. Алмаз очень прочный и твёрдый, графит – хрупкий. Элементарные ячейки алмаза и графита относятся к различным сингониям (рис. 1.19).

Рис. 1.19.Кристаллические решётки алмаза и графита

Оловоможет существовать в виде двух модификаций – серого и белого. Серое оловопри температурах ниже 13,3 °С. имеет решётку типа алмаза. При температурах выше 13,3 °С серое олово превращается в белое олово – очень хрупкое вещество, которое легко разрушается в порошок. Белое (металлическое) оловоимеет тетрагональную объёмноцентрированную решётку.

Полиморфные модификацииобозначают греческими буквами: α, β, γ, .., начиная с самой низкой температуры. Переход от одной модификации к другой сопровождается выделением или поглощением скрытой теплоты превращения. Полиморфное превращение является фазовым переходом 1-го рода. Полиморфизмимеет важное практическое значение: это свойство используется при термической обработке сталей, придании сталям различных свойств, получении нержавеющих сталей.

ИНДЕКСЫ МИЛЛЕРА

Для описания кристаллических многогранников и структур применяется метод индицирования.Через узлы кристаллической решетки можно провести прямые линии и плоскости. Выберем один из узлов решётки за начало координат.

Любой другой узел решётки определяется радиус–вектором:

R =ma +nb +рс .

Индексы узла– три простых числа [[mnp]], взятые в двойные квадратные или фигурные скобки (рис. 1.20). В системе параллельных прямых всегда можно выделить прямую линию (ряд), проходящую через начало координат. Тогда направление прямой линии определится двумя точками: началом координат и любым узлом ряда.

Индексы направления(прямой линии) – три простых числа [mnp], взятые в квадратные скобки. Эти числа характеризуют положение ближайшего узла, лежащего на прямой линии, проходящей через начало координат.

Рис. 1.20.Миллеровские индексы узлов

Проходящая сквозь узлы прямая, а также ребро кристаллического многогранника имеют наклон в выбранной системе координат. В целом плоские сетки в пространственной решётке и соответствующие им грани кристаллического многогранника имеют наклон в системе координат.

Пусть некоторая плоскость решётки пересекает все три оси координат, отсекая на них отрезки ma, nb, pc. Отношение чисел m:n:p характеризует наклон плоскости к осям координат. Серию отношений рациональных чисел m:n:p для всех параллельных плоскостей можно заменить отношением взаимно простых чисел р:q:r. Числа р, q, r называются параметрами Вейса.

Миллеровские индексы плоскости– три простых числа (HKL), записанные в круглых скобках. Индексы плоскости – дополнительные множители к величинам, обратно пропорциональным числу осевых единиц, отсекаемых любой плоскостью данного семейства на координатных осях Х, У, Z.

Миллеровские индексы определяются из соотношения чисел р:q:r.

Пусть некоторая плоскость отсекает на осях координат отрезки:

р =1, q = 3, c = 2 (рис. 1.21). Составим отношения:

p:q:c = 1:3:2

Общий знаменатель равен 6. Дополнительные множители: H = 6, K = 2, L = 3.

Миллеровские индексы данной плоскости (623).

Рис.1.21. Индексы плоскости(623)

Межплоскостное расстояние– это расстояние между параллельными плоскостями, содержащими одинаковое количество атомов. Чем больше индексы H, K, L, тем меньше расстояние между плоскостями. Для кубического кристалла межплоскостное расстояние d для параллельных плоскостей с одинаковыми индексами выражаются через индексы этих плоскостей соотношением:

а– постоянная решётки.

В 1819 г. Гаюи сформулировал законцелых чисел(теперь закон Гаюи): для любых двух граней реального кристалла двойные отношения параметров равны отношению малых чисел. На кристаллографическом многограннике образуются лишь такие грани, для которых двойные отношения отрезков, отсекаемых данной гранью и единичной гранью на трёх рёбрах кристалла, принятых за оси координат, равны отношению целых небольших простых чисел.

Грани, для которых отношение р:q:r является иррациональным, в реальном кристалле невозможны. Наклон всякой грани можно определить тремя целыми числами, если за оси координат выбрать направление трёх рёбер кристалла, а за параметры – отрезки, отсекаемые на этих осях данной гранью.

Рис. 1.11.Пространственные решётки некоторых веществ

Рис. 1.12.Линейная цепочка атомов

Ячейки сетки– параллелограммы, вершины которых являются узлами.

Рис. 1.13.Примитивная элементарная ячейка

Элементарные ячейкиразличаются по элементам симметрии и степени заполнения атомами (рис. 1.14).

Рис. 1.14.Разные примитивные ячейки в плоской сетке

Рис. 1.15. Элементы симметрии в кубическом кристалле

Рис. 1.16. Кристаллическая ячейка тетрагональной сингонии

Рис. 1.17. Кристаллические ячейки

Рис. 1.18.Решётки Браве

Рис. 1.19.Кристаллические решётки алмаза и графита

ИНДЕКСЫ МИЛЛЕРА

Любой другой узел решётки определяется радиус–вектором:

R =ma +nb +рс .

Рис. 1.20.Миллеровские индексы узлов

Миллеровские индексы определяются из соотношения чисел р:q:r.

Пусть некоторая плоскость отсекает на осях координат отрезки:

р =1, q = 3, c = 2 (рис. 1.21). Составим отношения:

p:q:c = 1:3:2

Общий знаменатель равен 6. Дополнительные множители: H = 6, K = 2, L = 3.

Миллеровские индексы данной плоскости (623).

Рис.1.21. Индексы плоскости(623)

а– постоянная решётки.

Дефекты кристаллического строения металлов

Точечные. Они бывают трех основных видов: вакансии, примеси или дислоцированные атомы. Приводят к ухудшению магнитных свойств металла, электро- и теплопроводности его.
Линейные, или дислокационные. Выделяют краевые и винтовые. Ухудшают прочность и качество материала.
Поверхностные дефекты. Влияют на внешний вид и структуру металлов.

Атомная кристаллическая решетка

Согласно своему названию, атомная кристаллическая решетка — это структура, в узлах которой расположены атомы. Они взаимодействуют с помощью ковалентных связей, то есть один атом отдает другому свободный электрон или же электроны из разных атомов образуют общую пару. В кристаллах с атомной решеткой частицы прочно связаны, что обуславливает ряд физических характеристик.

Свойства веществ с атомной решеткой:

прочность,
твердость,
неспособность к растворению в воде,
высокая температура кипения и плавления.

К примеру, атомную кристаллическую решетку имеет алмаз — самый твердый минерал в мире.

Другие примеры: германий Ge, кремний Si, нитрид бора BN, карборунд SiC. Типичный представитель этой группы — обычный песок, который по сути является оксидом кремния SiO

Лайфхак

Если нужно рассказать о свойствах веществ с атомной кристаллической решеткой, достаточно вспомнить песок и перечислить его характеристики.

Свойства металлов

К специфическим свойствам рассматриваемых веществ относят следующие.

Металлический блеск. Все представители простых веществ им обладают, причем большинство одинаковым серебристо-белым цветом. Лишь некоторые (золото, медь, сплавы) отличаются.
Ковкость и пластичность — способность деформироваться и восстанавливаться достаточно легко. У разных представителей выражена в неодинаковой мере.
Электропроводность и теплопроводность — одно из основных свойств, которое определяет области применения металла и его сплавов.

Кристаллическое строение металлов и сплавов объясняет причину каждого из обозначенных свойств и говорит о выраженности их у каждого конкретного представителя. Если знать особенности такого строения, то можно влиять на свойства образца и подстраивать его под нужные параметры, что и делают люди уже многие десятилетия.