Проекции геометрических тел с примерами и образцами выполнения

Формы геометрических тел

Деталь любой формы можно представить как совокупность отдельных геометрических тел.

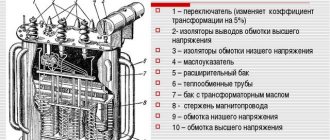
Для примера возьмем деталь (рис. 159. а) и проанализируем се форму. Мысленно разделив ее на отдельные элементы, получим следующие гео­метрические тела (рис. 159, б): 1 — усеченный прямой круговой конус с цилиндрическим отвер­стием, 2 — прямой круговой цилиндр, 3 — прямо­угольный параллелепипед, 4 — два прямоугольных параллелепипеда с цилиндрическими отверстия­ми, 5 — два полых полуцилиндра. Для выполне­ния комплексных чертежей необходимо усвоить методы проецирования отдельных геометрических тел, а также точек и линий, расположенных на поверхности этих тел.

Рис. 159

Геометрические тела, ограниченные плоскими многоугольниками, называются многогранниками (рис. 160, а). Эти многоугольники называются гранями, их пересечения — ребрами. Угол, образо­ванный гранями, сходящимися в одной точке — вершине, называется многогранным углом.

Тела вращения ограничены поверхностями, которые получаются в результате вращения ка­кой-либо линии вокруг неподвижной оси (рис. 160, б и в). Линия АВ, которая при своем движении образует поверхность, называется обра­зующей. Наиболее часто встречаются такие тела вращения, как цилиндр, конус, шар, тор.

Рис. 160

Проекции призм

Построение проекций правильной прямой шес­тиугольной призмы (рис. 161) начинается с выпо­лнения ее горизонтальной проекции — правильно­го шестиугольника. Из вершин этого шестиуголь­ника провопят вертикальные линии связи и строят фронтальную проекцию нижнего основания при­змы. Эта проекция изображается отрезком гори­зонтальной прямой. От этой прямой вверх откла­дывают высоту призмы и строят фронтальную проекцию верхнего основания. Затем вычерчива­ют фронтальные проекции ребер — отрезки верти­кальных прямых, равные высоте призмы. Фрон­тальные проекции передних и задних ребер совпа­дают. Горизонтальные проекции боковых граней изображаются в виде отрезков прямых. Передняя боковая грань 1243 изображается на плоскости V без искажения, а на плоскости W— в виде прямой линии. Фронтальные и профильные проекции остальных боковых граней изображаются с иска­жением.

На чертеже оси х, у и z не показывают, что делает чертеж более простым.

Рис. 161

Несколько сложнее построение проекций на­клонной призмы.

Рассмотрим порядок построения проекций на­клонной шестиугольной призмы.

1. Призма, основание которой лежит на плос­кости Н, наклонена к этой плоскости под утлом α (рис. 162, а). Ребра призмы параллельны плоскос­ти V, т.е. являются фронталями.

Вначале выполняется построение горизонталь­ной проекции основания призмы, которое проеци­руется на плоскость Н без искажения (правиль­ный шестиугольник). Фронтальная проекция осно­вания представляет собой отрезок прямой, парал­лельной оси х.

Из точек 1′, 2′, 3′ фронтальной проекции основания проводят прямые проекции ребер под углом α к оси х и на них откладывают действи­тельную длину бокового ребра призмы.

Строят фронтальную проекцию верхнего осно­вания призмы в виде отрезка прямой, равного и параллельного фронтальной проекции нижнего основания.

Из точек 1, 2, 3, 4. 5. 6 горизонтальной проек­ции нижнего основания проводят прямые — про­екции ребер — параллельно оси х и на них с по­мощью вертикальных линий связи находят шесть точек — горизонтальные проекции вершин верхне­го основания призмы.

2. Прямая правильная шестиугольная призма наклонена под углом α к плоскости Н. Основание призмы наклонено к плоскости Н под углом β (рис. 162, б).

В этом случае необходимо вначале построить фронтальную проекцию основания. Эта проекция представляет собой отрезок, равный расстоянию между параллельными сторонами шестиугольника. Если этот отрезок разделить пополам и из его середины провести линию связи, то на ней будут расположены точки 2 и 5 — горизонтальные про­екции вершин основания призмы. Расстояние между точками 2, 5 равно действительному рас­стоянию между вершинами основания призмы. Так как горизонтальные проекции сторон 16 и 34 представляют собой их действительные длины, то, воспользовавшись этим обстоятельством, мож­но построить полностью горизонтальную проек­цию основания.

Дальнейший процесс построения, показанный на рис. 162, б, аналогичен приведенному на рис. 162, а.

Рис. 162

На комплексных чертежах предметов часто приходится строить проекции линий и точек, расположенных на поверхности этих тел, имея только одну проекцию линии или точки. Рассмотрим решение такой задачи.

Дан комплексный чертеж четырехугольной пря­мой призмы и фронтальная проекция а’ точки А.

Прежде всего надо отыскать на комплексном чертеже две проекции грани, на которой располо­жена точка А. На комплексном чертеже видно (рис. 163, а), что точка А лежит на грани призмы 1265. Фронтальная проекция а’ точки А лежит на фронтальной проекции 1’2’6’5‘ грани призмы. Горизонтальная проекция 1562 этой грани — отре­зок 56. На этом отрезке и находится горизонталь­ная проекция а точки А. Профильную проекцию призмы и точки А строят, применяя линии связи.

По имеющемуся комплексному чертежу призмы можно выполнить ее изометрическую проекцию по координатам вершин. Для этого вначале строят нижнее основание призмы (рис. 163, б), а затем вертикальные ребра и верхнее основание (рис. 163, в).

По координатам т и п точки А, взятым с ком­плексного чертежа, можно построить аксономет­рическую проекцию этой точки.

Рис. 163

О правильном изображении конуса

Наверняка вам приходилось много раз изображать конус. Нарисуйте его еще раз. С большой степенью вероятности могу предположить, что картинка окажется неправильной. «А где здесь ошибка?» — спрашивают обычно школьники. «Эллипс, точка и две образующие. Как и в учебниках». Однако, не все так просто. Если ваш репетитор по математике знаком с методом изображений, то он вам скажет, что все без исключения рисунки в этих самых учебниках как раз то и неправильные. Когда рассказываешь об этом ученикам, интересно наблюдать за их реакцией. Сказанное репетитором по математике вызывает сначала легкое недоумение, удивление и даже недоверие, а затем естественное желание блеснуть знаниями перед своими сверстниками и удивить школьного преподавателя.

Где возникает ошибка? Давайте разберемся.

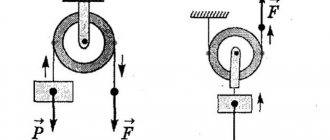
То, что мы рисуем в тетради – это проекции элементов конуса на выбранную плоскость, которую представляют расположенной в непосредственной близости от глаз. Фактически проецирование идет «в наши глаза». Вообразите себе прозрачный конус, в котором выделена линия основания и перпендикулярная к нему плоскость ABC осевого сечения. Если мы посмотрим на этот конус сбоку, то не увидим окружности в основании (это показано на рисунке слева). Вместо нее взору представится отрезок AС — основание равнобедренного треугольника в осевом сечении. Если взять непрозрачный конус, то мы увидим только половину его поверхности– ту часть, которая расположена перед плоскостью ABC.

Для того, чтобы открылась окружность основания (изображаемая в виде эллипса), необходимо немного повернуть ее плоскость по отношению к глазам. При маленьком угле мы увидим только ближнюю дугу основания, а дальняя будет закрыта треугольником ABC. Продолжая вращать конус, мы заставим вершину конуса (точку В) приближаться к глазам, треугольник ABC будет сужаться, постепенно открывая для просмотра заднюю, скрытую ранее часть поверхности конуса. Если угол поворота окажется равным , то получится противоположный эффект нулевому углу: основание увидим в форме окружности, а осевое сечение сольется в отрезок AC.В идеале нужно остановиться где-то между этими положениями. Тогда мы получим картинку, на которой часть дальней дуги AC будет закрыта треугольником ABC, а ее кусочки (около точек А и C) будут видны. Чем ближе угол поворота к нулю, тем эти кусочки менее заметны. Обратите внимание, на рисунке справа красной стрелкой показано место, где возникает ошибка. Даже при очень узком эллипсе в изображении основания можно увеличить рисунок в масштабе так, что кусочки дуги будут хорошо заметны. Это показывает красная стрелка на рисунке слева.

В этом состоит главная ошибка изобюражений конуса во всех без исключения школьных учебниках математики (и не только школьных): основание показано в виде эллипса (угол наклона достаточно приличный), а на выпирающие кусочки линии основания нет даже намека. Создается впечатление, что образующие AB и CB касаются эллипса. Однако это не так. Вот правильный рисунок:

Как репетитор по математике должен изображать конус?

Именно так, как это сделано в учебниках. И в методических и в математических целях правильный рисунок неудобен для практической работы. Почему?

1) Дальная дуга AC не пересекается с образующей в реальности, чего не скажешь об их проекциях. Мнимая точка пересечения на рисунке только помешает ученику рассматривать на чертеже какие-то более важные его элементы.

2) Реальные точки, попадающие в мнимое пересечение ни в каких задачах не участвуют. Их нет ни в условиях, ни в вопросах.

3) Если речь идет о преподаваниии в школе, то ученик с последней парты эти маленькие части дуги просто не увидит.

Замечание: есть хороший способ проверить уровень профессиональной подготовки репетитора математики: дать ему задание нарисовать конус в проекции по всем канонам и правилам. Если увидите знакомую картину – можно делать соответствующие выводы. Конечно, на занятиях со школьниками репетитор обязан «ошибаться», но это не освобождает его от знаний правил метода изображений.

Колпаков Александр Николаевич, репетитор математики, Москва.

Метки: Репетитор по стереометрии, Ученикам

Проекции пирамид

Построение проекций треугольной пирамиды начинается с построения основания, горизонталь­ная проекция которого представляет собой тре­угольник без искажения (рис. 164, а). фронталь­ная проекция основания — отрезок горизонталь­ной прямой.

Из горизонтальной проекции точки s (верши­ны. пирамиды) проводят вертикальную линию связи, на которой от оси х откладывают высоту пирамиды и получают фронтальную проекцию s’ вершины. Соединяя точку s’ с точками 1′, 2′ и 3′, получают фронтальные проекции ребер пира­миды.

Горизонтальные проекции ребер получают, соединяя горизонтальную проекцию точки s с горизонтальными проекциями точек 1, 2 и 3.

Пусть, например, дана фронтальная проекция а’ точки А, расположенной на грани пирамиды 1s2, и требуется найти другую проекцию этой точки. Для решения этой задачи проведем через а’ произвольную вспомогательную прямую и продолжим ее до пересечения с фронтальными проекциями 1’s’ и 2’s’ ребер в точках п’ и т‘. Затем проведем из точек п’ и т‘ линии связи до пересечения с горизонтальными проекциями 1s и 2s этих ребер в точках п и т. Соединив п с т, получим горизонтальную проекцию вспомогательной прямой, на которой с помощью линии связи найдем искомую горизонтальную проекцию а точки А Профильную проекцию этой точки нахо­дят по линиям связи.

Другой способ решения задачи на построение проекции точки по заданной ее проекции показан на рис. 164, б. Дана четырехугольная правильная пирамида. Через заданную фронтальную проек­цию а’ точки А проводят вспомогательную пря­мую, проходящую через вершину пирамиды и расположенную на ее грани. Горизонтальную проекцию ns вспомогательной прямой находят с помощью линии связи. Искомая горизонтальная проекция а точки А находится на пересечении линии связи, проведенной из точки а’, с горизон­тальной проекцией ns вспомогательной прямой.

Фронтальная диметрическая проекция рассмат­риваемой пирамиды выполняется следующим образом (рис. 164, в).

Вначале строят основание, для чего по оси х откладывают длину диагонали 13, а по оси у — половину длины диагонали 24. Из точки О пере­сечения диагоналей проводят ось z и на ней от­кладывают высоту пирамиды. Вершину S соединя­ют с вершинами основания прямыми линиями — ребрами.

Фронтальную диметрическую проекцию точки А, расположенной на грани пирамиды, строят по координатам, которые берут с комплексного чер­тежа. От качала координат О по оси х отклады­вают координату xА, из се конца параллельно оси у — половину координаты yА и из конца этой ко­ординаты параллельно оси z — третью координату zА. Построение точки В, расположенной на ребре пирамиды, более простое. От точки О по оси х от­кладывают координату xB и из конца ее проводят прямую, параллельную оси z, до пересечения с ребром пирамиды в точке В.

Рис. 164

Проекции цилиндров

Боковая поверхность прямого кругового цилин­дра получается вращением отрезка АВ образую­щей вокруг оси, параллельной этому отрезку. На рис. 165, а представлена изометрическая проекция цилиндра.

Построение горизонтальной и фронтальной проекций цилиндра показано на рис. 165, б и в.

Построение начинают с изображения основания цилиндра, т.е. двух проекций окружности (рис. 165, б). Так как окружность расположена на плоскости Н, то она проецируется на эту плос­кость без искажения. Фронтальная проекция ок­ружности представляет собой отрезок горизон­тальной прямой линии, равный диаметру окруж­ности основания.

После построения основания на фронтальной проекции проводят две очерковые (крайние) обра­зующие и на них откладывают высоту цилиндра. Проводят отрезок горизонтальной прямой, кото­рый является фронтальной проекцией верхнего основания цилиндра (рис. 165, в).

Рис. 165

Определение недостающих проекции точек А и В, расположенных на поверхности цилиндра, по заданным фронтальным проекциям в данном слу­чае затруднений нс вызывает, так как вся горизонтальная проекция боковой поверхности цилиндра представляет собой окружность (рис. 166. а). Следовательно, горизонтальные проекции точек А и В можно найти, проводя из данных точек а’ и b’ вертикальные линии связи до их пересечения с окружностью в искомых точ­ках а и Ь.

Профильные проекции точек А и В строят так­же с помощью вертикальных и горизонтальных линий связи.

Изометрическую проекцию цилиндра вычерчи­вают, как показано на рис. 166, б.

В изометрии точки A и В строят по координа­там. Например, для построения точки В от начала координат О по оси х откладывают координату xB = n, а затем через ее конец проводят прямую, параллельную оси у, до пересечения с контуром основания в точке 1. Из этой точки параллельно оси x проводят прямую, на которой откладывают координату xB = h1 точки В.

Рис. 166

Угол и площадь развертки

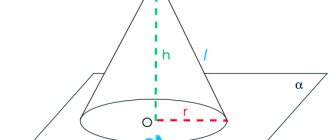
Теперь получим формулы, которые по известным параметрам g и r позволяют рассчитать площадь и угол развертки конуса.

Очевидно, что дуга кругового сектора, показанного выше на рисунке, имеет длину, равную длине окружности основания, то есть:

l = 2*pi*r.

Если бы весь круг радиусом g был построен, то его бы длина составила:

L = 2*pi*g.

Поскольку длина L соответствует 2*pi радианам, тогда угол, на который опирается дуга l, можно определить из соответствующей пропорции:

L ==> 2*pi;

l ==> φ.

Тогда неизвестный угол φ будет равен:

φ = 2*pi*l/L.

Подставляя выражения для длин l и L, приходим к формуле для угла развертки боковой поверхности конуса:

φ = 2*pi*r/g.

Угол φ здесь выражен в радианах.

Для определения площади Sb кругового сектора воспользуемся найденным значением φ. Составляем еще одну пропорцию, только уже для площадей. Имеем:

2*pi ==> pi*g2;

φ ==> Sb.

Откуда следует выразить Sb, а затем, подставить значение угла φ. Получаем:

Sb = φ*g2*pi/(2*pi) = 2*pi*r/g*g2/2 = pi*r*g.

Для площади конической поверхности мы получили достаточно компактную формулу. Величина Sb равна произведению трех множителей: числа пи, радиуса фигуры и ее образующей.

Тогда площадь всей поверхности фигуры будет равна сумме Sb и So (площадь круглого основания). Получаем формулу:

S = Sb + So = pi*r*(g + r).

Проекции конусов

Нагляднее изображение прямого кругового ко­нуса показано на рис. 167, а. Боковая поверхность конуса получена вращением отрезка BS вокруг оси, пересекающей отрезок в точке S. Последова­тельность построения двух проекций конуса пока­зана на рис. 167, б и в. Сначала строят две проекции основания. Горизонтальная проекция основа­ния — окружность. Фронтальной проекцией будет отрезок горизонтальной прямой, равный диаметру этой окружности (рис. 167, б). На фронтальной проекции из середины основания восставляют перпендикуляр и на нем откладывают высоту конуса (рис. 167, в). Полученную фронтальную проекцию вершины конуса соединяют прямыми с концами фронтальной проекции основания и по­лучают фронтальную проекцию конуса.

Рис. 167

Если на поверхности конуса задана одна проек­ция точки А (например, фронтальная проекция на рис. 168, а). то две другие проекции этой точки определяют с помощью вспомогательных линий — образующей, расположенной на поверхности ко­нуса и проведенной через точку А, или окружнос­ти, расположенной в плоскости, параллельной основанию конуса.

В первом случае (рис 168. а) проводят фрон­тальную проекцию s’a’f ’ вспомогательной обра­зующей. Пользуясь вертикальной линией связи, проведенной из точки f, расположенной на фрон­тальной проекции окружности основания, находят горизонтальную проекцию sf этой образующей, на которой с помощью линии связи, проходящей через а’, находят искомую точку а.

Во втором случае (рис. 168. б) вспомогательной линией, проходящей через точку А, будет окруж­ность. расположенная на конической поверхности и параллельная плоскости Н. Фронтальная проек­ция этой окружности изображается в виде отрезка Ь’с’ горизонтальной прямой, величина которого равна диаметру вспомогательной окружности. Искомая горизонтальная проекция а точки А на­ходится на пересечении линии связи, опущенной из точки а’, с горизонтальной проекцией вспомо­гательной окружности.

Если заданная фронтальная проекция Ь’ точки В расположена на контурной (очерко­вой) образующей SK, то горизонтальная проекция точки находится без вспомогательных линий (рис. 168. б).

В изометрической проекции точку А, находя­щуюся на поверхности конуса, строят по трем координатам (рис. 168, в): xА = n, yА = m, zА = h. Эти координаты последовательно откладывают по направлениям, параллельным изометрическим осям. В рассматриваемом примере от точки О по оси х отложена координата xА = n; из конца ее параллельно оси у проведена прямая, на которой отложена координата yА = m; из конца отрезка, равного т, параллельно оси z проведена прямая, на которой отложена координата zА = h. В резуль­тате построений получим искомую точку А.

Рис. 168

Что такое конус?

Конус — одно из основных тел вращения. Это тело образуется при повороте прямоугольного треугольника вокруг катета. В данном случае катет выступает в качестве оси симметрии и задает высоту конуса. Конус состоит из следующих элементов:

• основы — круглая форма;
• боковая поверхность.

Само построение конуса является очень простым, основная сложность состоит в создании материальности этой фигуры. У конуса также присутствует специфическая светотень, которую мы рассмотрим далее.

Проекции шара

На рис. 169, а изображена половина шара, сферическая поверхность этого шара образована вращением четверти окружности АВ вокруг ради­уса АО.

Проекции этой фигуры приведены на рис. 169, б. Горизонтальная проекция — окруж­ность радиуса, равного радиусу сферы, а фрон­тальная — полуокружность того же радиуса.

Если точка А расположена на сферической поверхности (рис. 169, в), то вспомогательная линия Ь’с’, проведенная через эту точку параллельно горизонтальной плоскости проекций, прое­цируется на горизонтальную плоскость проекций окружностью. На горизонтальной проекции вспо­могательной окружности находят с помощью ли­нии связи искомую горизонтальную проекцию а точки А.

Величина диаметра вспомогательной окружнос­ти равна фронтальной проекции Ь’с’.

Рис. 169

Проекции кольца и тора

Поверхность кругового кольца (рис. 170, а) образована вращением образующей окружности ABCD вокруг оси ОО1.

Тор — поверхность, образованная вращением части дуги окружности, являющейся образующей, вокруг оси ОО1, расположенной в плоскости этой окружности и не проходящей через ее центр.

Рис. 170

На рис. 171, а и б приведены два вида тора. В первом случае образующая дуга окружности радиуса R отстоит от оси вращения на расстоянии меньше радиуса R, а во втором случае — больше.

В обоих случаях фронтальные проекции тора представляют собой действительный вид двух образующих дуг окружности радиуса R, располо­женных симметрично относительно фронтальной проекции оси вращения. Профильными проекция­ми тора будут окружности.

Круговое кольцо (или открытый тор) имеет горизонтальную проекцию в виде двух концентри­ческих окружностей, разность радиусов которых равна толщине кольца или диаметру образующей окружности (рис. 170, б). Фронтальная проекция ограничивается справа и слева дугами полуокруж­ностей диаметра образующей окружности.

Рис. 171

В случае, когда точка А лежит на поверхности кругового кольца и дана одна се проекция, для нахождения второй проекции этой точки приме­няется вспомогательная окружность, проходящая через данную точку А и расположенная на повер­хности кольца в плоскости, перпендикулярной оси кольца (рис. 172).

Если задана фронтальная проекция а’ точки А, лежащей на поверхности кольца, то для нахожде­ния ее второй проекции (в данном случае — про­фильной) через а’ проводят фронтальную проек­цию вспомогательной окружности — отрезок вер­тикальной прямой линии b’c’. Затем строят про­фильную проекцию b»с» этой окружности и на ней, применяя линию связи, находят точку а“.

Если задана профильная проекция а» точки D, расположенной на поверхности этого кольца, то для нахождения фронтальной проекции точки D через d» проводят профильную проекцию вспомо­гательной окружности радиуса O»d“. Затем через верхнюю и нижнюю точки е» f» этой окружности проводят горизонтальные линии связи до пересечения с фронтальными проекциями образующей окружности радиуса r и получают точки e’ и f’. Эти точки соединяют вертикальной прямой, кото­рая представляет собой фронтальную проекцию вспомогательной окружности (она будет невиди­ма). Проводя горизонтальную линию связи из точки d» до пересечения с прямой e’f ‘, получаем искомую точку d’.

Такие же приемы построения применимы и для точек, находящихся на поверхности тора.

Рис. 172

Рисунок конуса

Конус представляет собой симметричное тело вращения, образующая конуса начинается в его вершине, совпадающей с осью вращения и заканчивается в основании. В нашем случае конус прямой, его ось перпендикулярна основанию.

При рисовании конуса сперва намечаем место и размер изображения в листе. Конус не должен быть слишком большим или маленьким, разместить его следует выше середины листа. Оптически верх конуса легче, вокруг него больше свободного пространства, поэтому конус в рисунке следует разместить выше, чем, это делается обычно.

Затем отмечаем засечкой самую верхнюю часть конуса и проводим горизонтальную ось основания. Определив таким образом высоту, определяем, насколько ширина основания меньше высоты. Рисуем засечки, ограничивающие ширину основания. При этом учитываем, что эллипс, после того, как он будет построен, немного увеличит высоту конуса.

Только после того, как определена высота и ширина, по центру проводим вертикальную ось симметрии.

Соединяем вершину конуса с основанием. Линии с краю являются самыми удалёнными от рисовальщика поверхностями, поэтому их следует рисовать светлыми.

Следующий этап — построение эллипса. При построении эллипса важно точно определить его раскрытость, насколько малый диаметр (видимый вертикальный размер) меньше, чем его ширина. Чтобы передать объём в линии, ближнюю часть овала сделаем темнее.

После того, как построение проверено, можно продолжить изображение объёмной формы конуса. Сперва находим границу света и тени. Граница представляет собой прямую линию, идущую от вершины к точке в основании. Постарайтесь верно определить, каково соотношение части, видимой на свету и части в тени. В верхней части линия немного чётче, в нижней части конуса она более плавно размыта к краям. Связано это с тем, что ближе к вершине конуса форма заворачивается сильнее, она почти приближается к угловой форме, какую мы видим на примере куба. Теневая поверхность удаляется от нас, дальний край по закону воздушной перспективы будет светлее.

Освещённая часть удаляется от зрителя, поэтому, в соответствии с законами воздушной перспективы, она будет темнее. На границе света и тени мы видим полутон, промежуточную поверхность между светом и тенью, он относится к свету, но темнее, чем освещённая часть предмета, т. к. угол падения лучей света здесь небольшой. Падающая тень темнее тени собственной. Она лежит на горизонтальной поверхности, передняя часть тени темнее. Штрих кладём по форме, сначала в направлении лучей, идущих от вершины к основанию.

Для лучшей передачи формы введём горизонтальные линии штриховки, показывающие сечение формы по горизонтали. Особенно важно показать, как форма заворачивается по краям. На завершающем этапе работы уточняем тональные отношения и форму. Освещённая часть чуть темнее снизу, сверху выше контраст света и тени. Теневая часть конуса снизу подсвечена рефлексом от поверхности стола, также имеется рефлекс, проходящий по дальнему краю формы.