Понятие
Принципы образования геометрического тела просты. Представим две параллельные плоскости a и a1. С расположенной на первой точке перпендикуляр опускается на вторую. Точка на a1 – основание перпендикуляра, она является центром круга. Если соединить точку на плоскости a с каждой точкой круга на a1, получится конус. Основание перпендикуляра его – высота.
Второй вариант образования рассматриваемого геометрического тела: прямоугольный треугольник вращается вокруг катета по или против часовой стрелки. Катет, ставший осью, будет высотой конуса, лежащий в основании – диаметром нижней поверхности, гипотенуза – образующей.
Длина образующих одинакова, их совокупность называется боковой поверхностью. Квадрат длины образующей равняется сумме квадратов высоты и радиуса основания (из теоремы Пифагора): l2 = h2 + r2. Отсюда
Какую фигуру будем изучать?
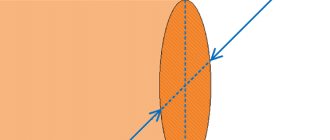
Круглый прямой усеченный конус представляет собой два круга, имеющих разный диаметр, которые расположены в параллельных плоскостях. Окружности этих кругов соединены прямыми отрезками равной длины, именуемых образующими фигуры. Расстояние между круглыми основаниями называется высотой. Описанная фигура показана ниже на фото.
Получить ее можно двумя принципиально отличающимися геометрическими способами. Во-первых, можно взять обычный круглый конус и параллельной его основанию плоскостью отсечь верхнюю часть. Такое действие приведет к образованию верхнего (малого) основания усеченного конуса. Во-вторых, можно взять трапецию с двумя прямыми углами и вращать ее вокруг стороны, ограниченной этими углами. Сторона трапеции, вокруг которой будет происходить вращение, называется осью фигуры. Две параллельные стороны трапеции опишут круглые основания во время вращения, а четвертая наклонная сторона образует боковую поверхность фигуры.
Схема выше демонстрирует получение усеченного конуса с помощью сечения плоскостью.
Разновидности конусов
В геометрии насчитывают почти десяток типов конусов:
- Прямой круговой – нижняя грань представлена кругом – фигурой, имеющей центр симметрии. Ось, которая проходит от вершины к центру основания, перпендикулярна плоскости последнего.
- Наклонный либо косой – проекция вершины на нижнюю поверхность не совпадает с его центром.
- Круговой – с кругом в центре.
- Прямой – нижняя поверхность представлена кругом либо эллипсом. Центр нижней поверхности совпадает с проекцией вершины на неё.
- Гиперболический, параболический, эллиптический – опираются на соответствующие фигуры.
- Равносторонний – образующая равна диаметру нижней поверхности.
- Усеченный – ограниченный плоскостью, параллельной основанию. Располагается между ним и вершиной геометрического тела.
- Двойной – два одинаковых тела имеют общую вершину или основание и ось – проходит через оба тела.
Сечение плоскостью призмы, пирамиды, цилиндра и конуса
СЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ТЕЛ ПЛОСКОСТЬЮ
В заданиях на построение усеченных геометрических тел можно выделить следующие задачи: 1) построение усеченного тела в системе трех плоскостей проекций; 2) определение истинной величины фигуры сечения; 3) построение развертки усеченного тела и 4) вычерчивание его аксонометрической проекции. Ниже помещены рекомендации по решению каждой из перечисленных задач.
Вначале по положению секущей плоскости определяют вид фигуры сечения и в зависимости от формы геометрического тела выбирают прием построения проекций сечения. В заданиях секущие плоскости занимают проецирующее положение, поэтому одна проекция сечения задается. Недостающие проекции фигуры сечения призмы или пирамиды строят по точкам пересечения их ребер с заданной плоскостью. Если же плоскость пересекает поверхность вращения по лекальной кривой, то начинают с определения ее характерных точек.
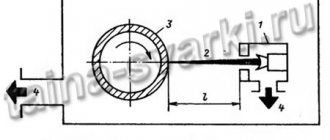
Например, фронтально проецирующая плоскость Р (рис. 106) пересекает цилиндр по неполному эллипсу. Его характерными точками являются: 1) А и В — точки, принадлежащие линии пересечения плоскости Р с основанием цилиндра; 2) С — конец большой оси эллипса; 3) D и Е — концы малой оси эллипса и они же точки, лежащие на очерковых образующих цилиндра Последовательность нахождения точек эллипса указана стрелками на примере промежуточных точек 1 и 2.
Рис. 106
Истинную величину фигуры сечения определяют с помощью способа перемены плоскостей проекций или вращения. Если применяют способ перемены плоскостей проекций, то дополнительную плоскость задают параллельно секущей плоскости. Дополнительную плоскость совмещают с основной плоскостью проекций так, чтобы новая проекция сечения не наложилась на имеющиеся проекции. При использовании способа вращения ось вращения целесообразно располагать в секущей плоскости и на некотором расстоянии от тела.
Для примера показано положение оси вращения U (рис. 107) при определении истинной величины сечения четырехугольной призмы фронтально проецирующей плоскостью Р.
Рис. 107
Построение развертки усеченного тела начинают с вычерчивания развертки его полной боковой поверхности. Далее на нее наносят линии сечения и пристраивают к ней остальные части развертки — основания и фигуру сечения. Если какие-либо элементы, необходимые для построения развертки, на проекциях искажены, то предварительно определяют их истинную величину.
Рис. 108
Например, для построения развертки правильной усеченной четырехугольной пирамиды (рис. 108) необходимо определить истинную величину фигуры сечения — треугольника ADE и длину одного из ее боковых ребер, например ребра SB. Для определения истинной величины этих элементов их поворачивают до положения, параллельного плоскости V. Треугольник ADE повернут вокруг оси U, а ребро SB — вокруг высоты пирамиды. Далее строят развертку согласно рекомендациям в следующем порядке: задают положение вершины S; вычерчивают развертку полной боковой поверхности пирамиды; наносят на нее линии сечения DE и AE с помощью отрезков SE = = s′e′1 = L2и DC = dc; пристраивают к ребру основания АВ фигуру усеченного основания— четырехугольник ABCD = abcd и к его стороне AD — треугольник ADE = a′1e′1 d′1.
Усеченные тела на аксонометрической проекции вначале вычерчивают целыми. Далее изображают проекцию сечения и контурными линиями обводят усеченную часть тела.
Рис. 109
Для примера на рис. 109 вычерчена изометрическая проекция конуса, усеченного фронтально проецирующей плоскостью Р по параболе. Параболу на изометрической проекции начинают строить с ее вершины А. Эту точку получают с помощью координаты—хА. Проекции нижних точек параболы В и С строят по координате хВ,С. Соединив точку А с серединой отрезка ВС, получают проекцию оси симметрии параболы. Для построения ее промежуточных точек откладывают по оси конуса от его основания отрезки, равные координатам z1,2, z3,1, z5,6. Через концы отложенных отрезков проводят прямые, параллельные оси координат X, до пересечения с осью симметрии параболы. Через полученные точки проводят хорды параболы, которые параллельны ее нижней хорде ВС. Длину каждой хорды замеряют на горизонтальной проекции усеченного конуса и откладывают на соответствующей хорде изометрической проекции.
Задание 23. Усеченные геометрические тела. Построить заданные усеченные геометрические тела (призму, пирамиду, цилиндр, конус) в системе трех плоскостей проекций, определить истинные величины фигур сечения, вычертить развертки усеченных тел и их аксонометрические проекции. Вид аксонометрической проекции указан в табл. 13.
Таблица 13
| Варианты задания | Прямоугольная изометрическая проекция | Прямоугольная диметрическая проекция |
| номера задач | ||
| I, III, V, VII, IX, XI, XIII, XV | 1, 3 | 2, 4 |
| II, IV, VI, VIII, X, XII,XIV | 2, 4 | 1, 3 |
| XVI | 1, 4 | 2, 3 |
Изображение каждого геометрического тела располагают на листе формата A3.
Образцы выполненного задания с разными вариантами оформления приведены на рис. 110—113.
Рис.110
Рис. 111
Рис. 112
Рис. 113
Работу над заданием следует начинать с компоновки чертежа, которая довольно трудоемка из-за большого количества изображений. Габариты горизонтальной, фронтальной, профильной и аксонометрической проекций тела подсчитывают по заданным проекциям. Размеры сечения и развертки определяют приблизительно или делают на черновике нужные построения.
Сократить работу с предлагаемым заданием можно, уменьшив число геометрических тел или упростив содержание задания. Например, отказаться от вычерчивания аксонометрической проекции тела или не строить его развертку.
СЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ТЕЛ ПЛОСКОСТЬЮ
В заданиях на построение усеченных геометрических тел можно выделить следующие задачи: 1) построение усеченного тела в системе трех плоскостей проекций; 2) определение истинной величины фигуры сечения; 3) построение развертки усеченного тела и 4) вычерчивание его аксонометрической проекции. Ниже помещены рекомендации по решению каждой из перечисленных задач.
Вначале по положению секущей плоскости определяют вид фигуры сечения и в зависимости от формы геометрического тела выбирают прием построения проекций сечения. В заданиях секущие плоскости занимают проецирующее положение, поэтому одна проекция сечения задается. Недостающие проекции фигуры сечения призмы или пирамиды строят по точкам пересечения их ребер с заданной плоскостью. Если же плоскость пересекает поверхность вращения по лекальной кривой, то начинают с определения ее характерных точек.
Например, фронтально проецирующая плоскость Р (рис. 106) пересекает цилиндр по неполному эллипсу. Его характерными точками являются: 1) А и В — точки, принадлежащие линии пересечения плоскости Р с основанием цилиндра; 2) С — конец большой оси эллипса; 3) D и Е — концы малой оси эллипса и они же точки, лежащие на очерковых образующих цилиндра Последовательность нахождения точек эллипса указана стрелками на примере промежуточных точек 1 и 2.
Рис. 106
Истинную величину фигуры сечения определяют с помощью способа перемены плоскостей проекций или вращения. Если применяют способ перемены плоскостей проекций, то дополнительную плоскость задают параллельно секущей плоскости. Дополнительную плоскость совмещают с основной плоскостью проекций так, чтобы новая проекция сечения не наложилась на имеющиеся проекции. При использовании способа вращения ось вращения целесообразно располагать в секущей плоскости и на некотором расстоянии от тела.
Для примера показано положение оси вращения U (рис. 107) при определении истинной величины сечения четырехугольной призмы фронтально проецирующей плоскостью Р.
Рис. 107
Построение развертки усеченного тела начинают с вычерчивания развертки его полной боковой поверхности. Далее на нее наносят линии сечения и пристраивают к ней остальные части развертки — основания и фигуру сечения. Если какие-либо элементы, необходимые для построения развертки, на проекциях искажены, то предварительно определяют их истинную величину.
Рис. 108
Например, для построения развертки правильной усеченной четырехугольной пирамиды (рис. 108) необходимо определить истинную величину фигуры сечения — треугольника ADE и длину одного из ее боковых ребер, например ребра SB. Для определения истинной величины этих элементов их поворачивают до положения, параллельного плоскости V. Треугольник ADE повернут вокруг оси U, а ребро SB — вокруг высоты пирамиды. Далее строят развертку согласно рекомендациям в следующем порядке: задают положение вершины S; вычерчивают развертку полной боковой поверхности пирамиды; наносят на нее линии сечения DE и AE с помощью отрезков SE = = s′e′1 = L2и DC = dc; пристраивают к ребру основания АВ фигуру усеченного основания— четырехугольник ABCD = abcd и к его стороне AD — треугольник ADE = a′1e′1 d′1.
Усеченные тела на аксонометрической проекции вначале вычерчивают целыми. Далее изображают проекцию сечения и контурными линиями обводят усеченную часть тела.
Рис. 109
Для примера на рис. 109 вычерчена изометрическая проекция конуса, усеченного фронтально проецирующей плоскостью Р по параболе. Параболу на изометрической проекции начинают строить с ее вершины А. Эту точку получают с помощью координаты—хА. Проекции нижних точек параболы В и С строят по координате хВ,С. Соединив точку А с серединой отрезка ВС, получают проекцию оси симметрии параболы. Для построения ее промежуточных точек откладывают по оси конуса от его основания отрезки, равные координатам z1,2, z3,1, z5,6. Через концы отложенных отрезков проводят прямые, параллельные оси координат X, до пересечения с осью симметрии параболы. Через полученные точки проводят хорды параболы, которые параллельны ее нижней хорде ВС. Длину каждой хорды замеряют на горизонтальной проекции усеченного конуса и откладывают на соответствующей хорде изометрической проекции.
Задание 23. Усеченные геометрические тела. Построить заданные усеченные геометрические тела (призму, пирамиду, цилиндр, конус) в системе трех плоскостей проекций, определить истинные величины фигур сечения, вычертить развертки усеченных тел и их аксонометрические проекции. Вид аксонометрической проекции указан в табл. 13.
Таблица 13
| Варианты задания | Прямоугольная изометрическая проекция | Прямоугольная диметрическая проекция |
| номера задач | ||
| I, III, V, VII, IX, XI, XIII, XV | 1, 3 | 2, 4 |
| II, IV, VI, VIII, X, XII,XIV | 2, 4 | 1, 3 |
| XVI | 1, 4 | 2, 3 |
Изображение каждого геометрического тела располагают на листе формата A3.
Образцы выполненного задания с разными вариантами оформления приведены на рис. 110—113.
Рис.110
Рис. 111
Рис. 112
Рис. 113
Работу над заданием следует начинать с компоновки чертежа, которая довольно трудоемка из-за большого количества изображений. Габариты горизонтальной, фронтальной, профильной и аксонометрической проекций тела подсчитывают по заданным проекциям. Размеры сечения и развертки определяют приблизительно или делают на черновике нужные построения.
Сократить работу с предлагаемым заданием можно, уменьшив число геометрических тел или упростив содержание задания. Например, отказаться от вычерчивания аксонометрической проекции тела или не строить его развертку.
Площадь
Под площадью подразумевают количество квадратов со стороной единица, помещающихся на определенной поверхности.
Площадь прямого конуса определяется по формуле:
- основания – Sосн = πr2; r – радиус;
- боковой поверхности – Sбп = πrl; l – длина;
- полная – S = Sосн + Sбп = πr2 + πrl = πr (r + l).
Пример:
- диаметр равен 12 см;
- длина образующей – 10 см.
Решение.
Радиус – это половина диаметра: 12/2 = 6 см.
Подставим значения в выражение: S = πr (r + l).
Получим: S = π * 6 *(6 + 10) = 96 π ≈ 301,584 см2.
Объем усечённого конуса
Объем – пространство, занимаемое геометрическим телом. Численное значение указывает на количество кубиков с гранью единица, помещающихся в конусе. Объем тела вычисляется как треть произведения площади основания на его высоту.
Основание – круг, его поверхность рассчитывается по формуле: Sосн = πr2. После подстановки получим:
.
Пример: вычислить объем тела: r = 6 см, h = 9 см. Ставим значения в формулу, пошагово упрощаем выражение.
Если известен диаметр, разделите его на два: .
Вычислим объем усеченного конуса. Для понимания, от полного объема исходного тела нужно отнять значение отрезанного параллельной нижней грани плоскостью.
Формула объема усеченного конуса:
Задача 5
Рис. 8. Вращаемый треугольник
Рис. 9. Тело, полученное при вращении равнобедренного треугольника
Равнобедренный треугольник, боковая сторона которого равна , а угол при основании равен , вращается вокруг своего основания (см. рис. 8). Найти площадь поверхности полученного при вращении тела (см. рис. 9).
Решение
Рис. 10. Два равных конуса
Если провести в треугольнике высоту из вершины, то получается два прямоугольных треугольника, вращая которые мы получаем два равных конуса, прилегающих друг к другу основаниями (см. рис. 10).
Значит, площадь поверхности искомого тела равна удвоенной площади боковой поверхности любого из конусов. Таким образом, нам надо найти радиус основания и образующую конуса (см. рис. 11).
Рис. 11. Иллюстрация к последнему шагу
Радиус основания конуса равен высоте исходного треугольника, а образующая – боковой стороне. Очевидно, высота равна , а значит, , таким образом, окончательный ответ: .
Ответ: .